# 介绍

数据保护最近引起了越来越多的关注，并且已经提出了一些法规来保护个人用户的隐私。在这些法规中，提到了「被遗忘权」，它赋予数据主体从存储数据的实体中删除其数据的权利。这也意味着在机器学习中，模型提供者有义务消除其所有者要求被遗忘的数据的任何影响，即遗忘学习。

最简单和有效的遗忘学习方法就是移除对应的样本后重新训练模型，然而当底层数据集很大时，这种方法在计算上可能令人望而却步。目前通用的遗忘学习方法是SISA (Sharded, Isolated, Sliced, and Aggregated) ——将训练集分为shards, shards中分为slices, 对于每个slice训练之后记录model parameters, 每个数据点被划分到不同的shards和slices中, unlearn时就是排除掉对应数据点然后retrain对应的shard和slices, 以空间开销换取训练的时间开销。

对于图像和文本数据，分割数据没有什么问题。然而，对于图来说，GNN依赖于图结构信息，像在SISA中那样将节点随机划分为子图可能会严重损坏生成的模型。对此，作者提出了GraphEraser，以实现GNN中的遗忘学习。

作者将图遗忘学习分为node unlearning「节点遗忘学习」和edge unlearning「边遗忘学习」，提出了两种图分割策略。第一种侧重于graph structural information「图结构信息」，另一种则是同时考虑graph structural and node feature information「图结构和节点特征信息」。

为了同时考虑图结构和节点特征信息，作者将节点特征和图结构转化为嵌入向量，然后将其聚类为不同的shards。但是由于现实世界图的结构特性，传统的群落检测和聚类方法划分会导致分片大小不平衡，而大部分需要被撤销的数据都在最大的分区，从而导致效率低下。作者提出了两种分割算法和一种聚合算法以解决此问题。

# 贡献

• 第一次提出了在GNN模型上的遗忘学习方法
• 提出了两种算法以平衡图分割块大小
• 提出了一种基于学习的聚合方法

# 问题构造

# 问题定义

节点遗忘学习

对于GNN模型$F_o$，每个数据主体的数据对应于GNN训练图$G_o$中的一个节点。数据主体$u$要删除其所有数据，则意味着从GNN的训练图中遗忘学习$u$的节点特征以及其于其他节点的链接。以社交网络为例，节点遗忘学习意味着需要从目标GNN的训练图中删除用户的个人资料信息和社交关系。

边遗忘学习

数据主体$u$要删除其节点于另一个节点$v$之间的一条边缘。仍然以社交网络为例，边缘遗忘意味着社交网络用户想要隐藏他们与另一个人的关系。

# 评估指标

• unlearning efficiency「遗忘学习效率」：与在训练的时间有关，时间要尽可能短。
• model utility「模型效用」：与准确性有关，越高越好。

在之前提过，图分割存在分片大小不均匀的问题。为此，作者提出了两种分片目标：

• G1: Balanced Shards「均衡分片」：每个分片中的节点数量相似。这样，每个分片的再训练时间是相似的，从而提高了整个图遗忘学习过程的效率。
• G2: Comparable Model Utility「可比模型效用」：图结构信息是决定GNN性能的主要因素，每个分片都应保留图的结构属性。

# GraphEraser框架构造

作者将GraphEraser框架分为三个阶段：

• Balanced Graph Partition「平衡图分区」：将训练图划分为不相交的分片
• Shard Model Training「分片训练模型」：对每个分片进行训练一个模型，称之为shard model「分片模型」$F_i$
• Shard Model Aggregation「分片模型聚合」：为了得到预测节点$w$的标签，将对应的数据（$w$的特征、其邻居的特征以及其中的图结构）同时发送到所有分片模型，并通过聚合所有分片模型的预测来获得最终预测。

GraphEraser框架的结构图如下所示：

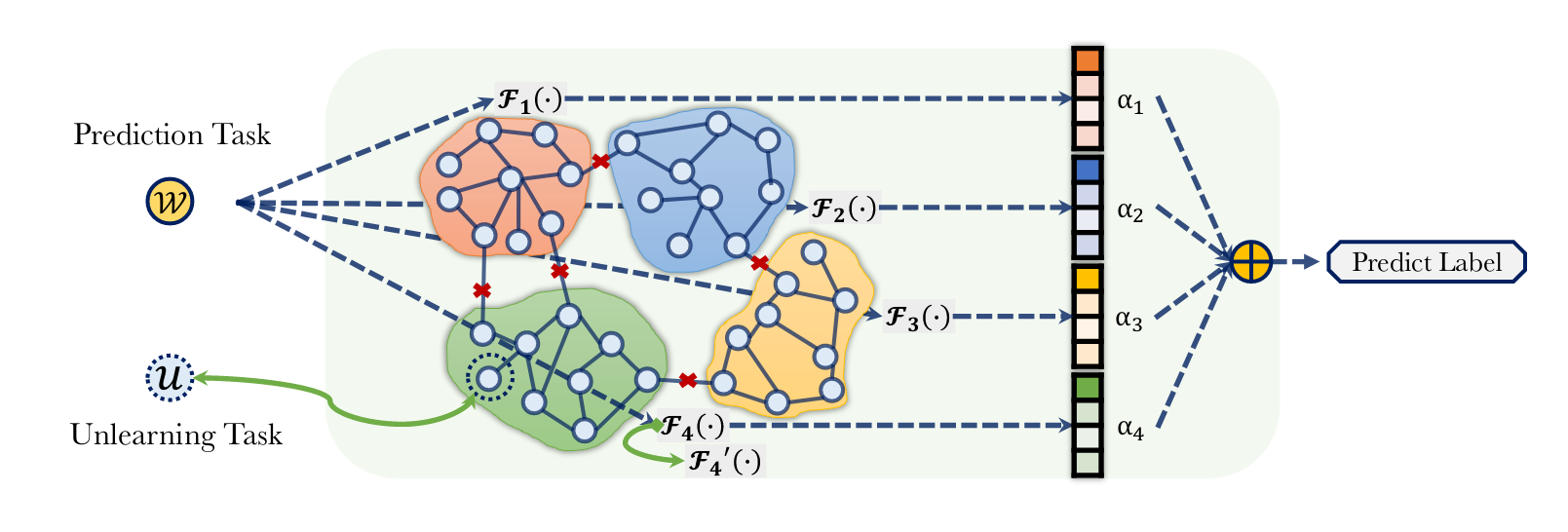
# 平衡图分割

作者提出了三种图分区策略：

• 策略0：仅考虑节点特征信息，并随机对节点进行分区

  该策略可以满足G1「均衡分片」要求，但不满足G2「可比模型效用」要求

• 策略1：依靠community detection「社区发现」，仅考虑结构信息，并尽可能保留它

• 策略2：同时考虑结构信息和节点特征。将节点特征和图结构表示为低维向量，即节点嵌入，然后将节点嵌入聚类到不同的分片中。

  直接这样划分会导致划分区域不平衡，如下图所示：

  

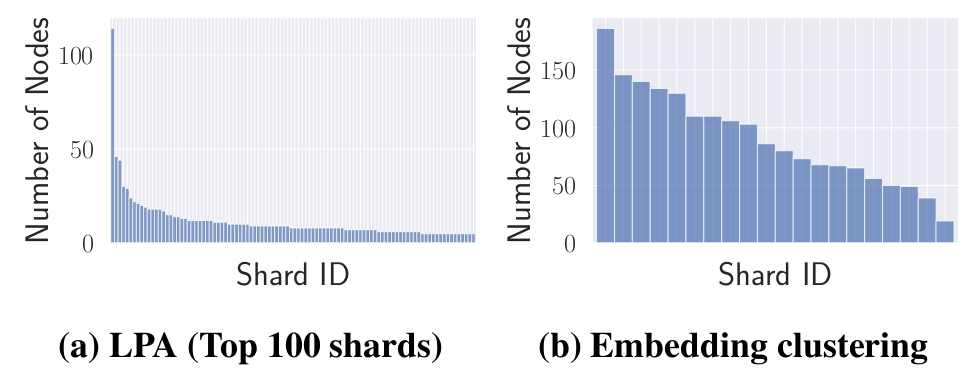
接下来，作者便介绍了对应的平衡图分区算法。

# 社区发现算法

对于策略1，主要依赖的就是此算法。作者基于Label Propagation Algorithm (LPA)「标签传播算法」来设计图分区算法。在本文中，shard就是community。

标签传播算法

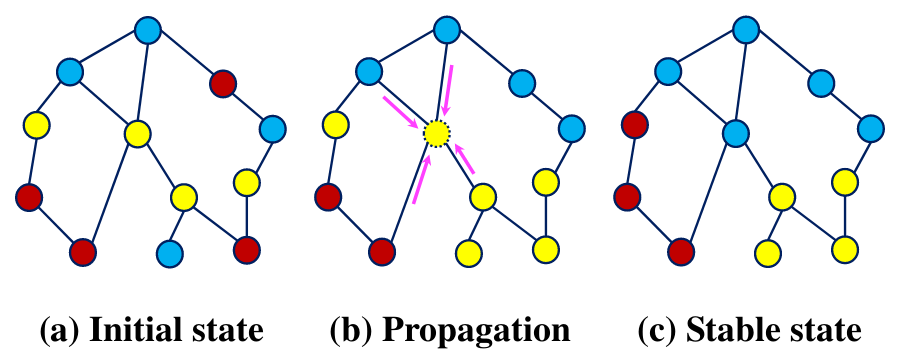
在初始阶段（图a），每个节点都随机分配一个分片标签。

在标签传播阶段（图b → 图 c），每个节点都会发送自己的标签，将自己更新成收到最多的那个标签

标签传播过程会对所有节点进行多次迭代，直到收敛（没有节点更改标签）

就如之前提到的，传统的LPA会导致高度不平衡的图形分区，严重影响了遗忘学习的效率。

对此，作者提出了一个实现平衡图分区的一般方法。给定所需的分片大小$k$和最大分片大小$\delta$，为每个节点-分片定义一个可能被分配到此分片的preference「偏好值」，代表该节点被分配给了分片（这被称为destination shard「目标分片」），从而产生$k \times n$个偏好值。对这些值进行排序，如果目标分片中的节点数不超过$\delta$，就将该节点分配给此分片。

具体而言，作者提出了Balanced LPA (BLPA)「平衡标签传播算法」，将偏好值定义为节点分片对的neighbor counts「邻居计数」（属于目标分片的邻居数量），并且具有较大邻居计数的节点分片对具有更高的优先级分配。

算法的步骤如下：

1. 初始化：将每个节点随机分配给k个分片之一
2. 重新分配配置文件计算：对于每个节点$u$，使用元组$\left\langle u, \mathbb{C}_{s r c}, \mathbb{C}_{d s t}, \xi\right\rangle$表示其重新分配的配置文件，其中$\mathbb{C}_{s r c}$和$\mathbb{C}_{d s t}$是节点$u$的当前分片和目标分片，$\xi$是目标分片$\mathbb{C}_{d s t}$的邻居计数，并将其存入$\mathbb{F}$
3. 排序：邻居数量越多的重新分配配置文件应具有越高的优先级，所以按$\xi$对$\mathbb{F}$进行降序排序
4. 传播标签：枚举$\mathbb{F}$里的所有元素，如果$\mathbb{C}_{d s t}$的大小不超过给定的阈值$\delta$，就将其添加到目标分片并从当前分片中删除。之后在$\mathbb{F}$中删除所有剩余的包含节点$u$的元组。

之后不断迭代，直到分片不更改或达到最大迭代$T$

算法的时间复杂度为$O(n·d_{ave})$，$n$为节点数，$d_{ave}$为训练图的平均节点数。

作者无法从理论上证明其收敛性，不过通过实验表示$T=30$时几乎是收敛的。

# 嵌入式聚类算法

对于策略2，作者使用预训练的GNN模型来获取所有节点嵌入，然后对生成的节点嵌入执行聚类。

思路是将GNN模型的所有节点投影到空间中，再使用K-Means进行聚类。同样也会导致分块的不平均这个问题。

对此，作者提出了Balanced Embedding k-means (BEKM)。定义preference「偏好值」为节点嵌入和所有节点分片对的分片质心之间的欧氏距离。

具体的算法如下：

1. 初始化：随机选择$k$个质心$C^0=\{C^0_1,C^0_2,\dots,C^0_k\}$
2. 计算嵌入质心距离：计算节点嵌入和质心之间的所有成对距离，从而得到$n\times k$个嵌入质心对。这些对存储在$\mathbb{F}$中。
3. 排序质心距离：距离较近的嵌入质心对具有更高的优先级，所以按照升序对$\mathbb{F}$进行排序
4. 重新分配节点和更新质心：枚举$\mathbb{F}$里的所有元素，如果$\mathbb{C}_{j}$的大小不超过给定的阈值$\delta$，就将其添加到目标分片。之后在$\mathbb{F}$中删除所有剩余的包含节点$i$的元组。最后，将新质心计算为其相应分片中所有节点的平均值。

同样，不断重复直到分片不更改或达到最大迭代$T$

算法的时间复杂度为$O(k·n)$，$n$个节点,$k$个分片。

# 基于学习的聚合

目前常见的聚合方式有两种：

• MajAggr：每个分片模型预测一个标签，取最多预测的标签
• MeanAggr：收集所有分片模型的后验向量，然后求平均值，得到聚合后验，选取最高后验值。

作者提出了一种基于学习的聚合方法LBAggr，为每个分片模型分配一个重要性分数，通过以下损失函数进行学习：

$$\min _{\alpha} \underset{w \in \mathcal{G}_{o}}{\mathbb{E}}\left[\mathcal{L}\left(\sum_{i=0}^{m} \alpha_{i} \cdot \mathcal{F}_{i}\left(X_{w}, \mathcal{N}_{w}\right), y\right)\right]+\lambda \sum_{i=0}^{m}\left|\alpha_{i}\right|$$

其中$X_{w}$和$\mathcal{N}_{w}$是训练图中节点$w$的特征向量和邻域，$y$是$w$的真实标签，$\mathcal{F}_{i}(\cdot)$表示分片模型$i$，$\alpha_{i}$是$\mathcal{F}_{i}(\cdot)$的重要性得分，$m$是分片总数。将所有重要性分数的总和调节为 1。

作者通过梯度下降来找到最优的$\alpha$，从而解决最优化问题。然而，直接梯度下降会导致$\alpha$为负数。为了解决此问题，作者使用softmax 函数在每次迭代中进行归一化处理。

为了提升运行速度，作者指出可以使用训练图中 10% 的节点进行重新训练。

# GraphEraser

将上面提到的方法集合在一起，就得到了此算法。当某些节点或边缘被数据所有者撤销时，只需要重新训练相应的分片模型即可。

# 评估

数据集

作者采用了五个常用的图像数据集，分别为Cora, Citeseer, Pubmed, CS和Physics。

模型

作者在四个GNN模型上进行了测试，分别是SAGE，GCN，GAT和GIN。每个模型都经过100轮的训练，默认学习率设置为0.01，权重衰减为0.001。

指标

在问题构造中提过，就是遗忘学习效率和模型效用

• 遗忘学习效率：计算100个独立遗忘学习请求的平均遗忘学习时间。
• 模型效用：使用F1得分

基线

• Scratch「从头开始训练」
• Random「随机分区」

实验设置

将整个图分为两个不相交的部分，其中80%的节点用于训练GNN模型，20%的节点用于评估模型效用。

分片大小$k$设为20, 20, 50, 30, 和 100

片中节点最大个数$\delta$设为$\left \lceil \frac{n}{k} \right \rceil $

最大迭代次数$T$设为30

BLPA对应社区发现算法；BEKM对应嵌入式聚类算法

# 遗忘学习效率评估

如图所示，BLPA和BEKM相对于从头训练模型，可以显著的减少训练的时间。

相对于Random，时间略长是因为存在更长的图分割成本。BLPA 和 BEKM 都需要多次迭代以保留结构信息。但一旦完成图分割，就会将其固定下来。从这个意义上说，我们可以容忍这种代价，因为它只执行一次。

# 模型效用评分

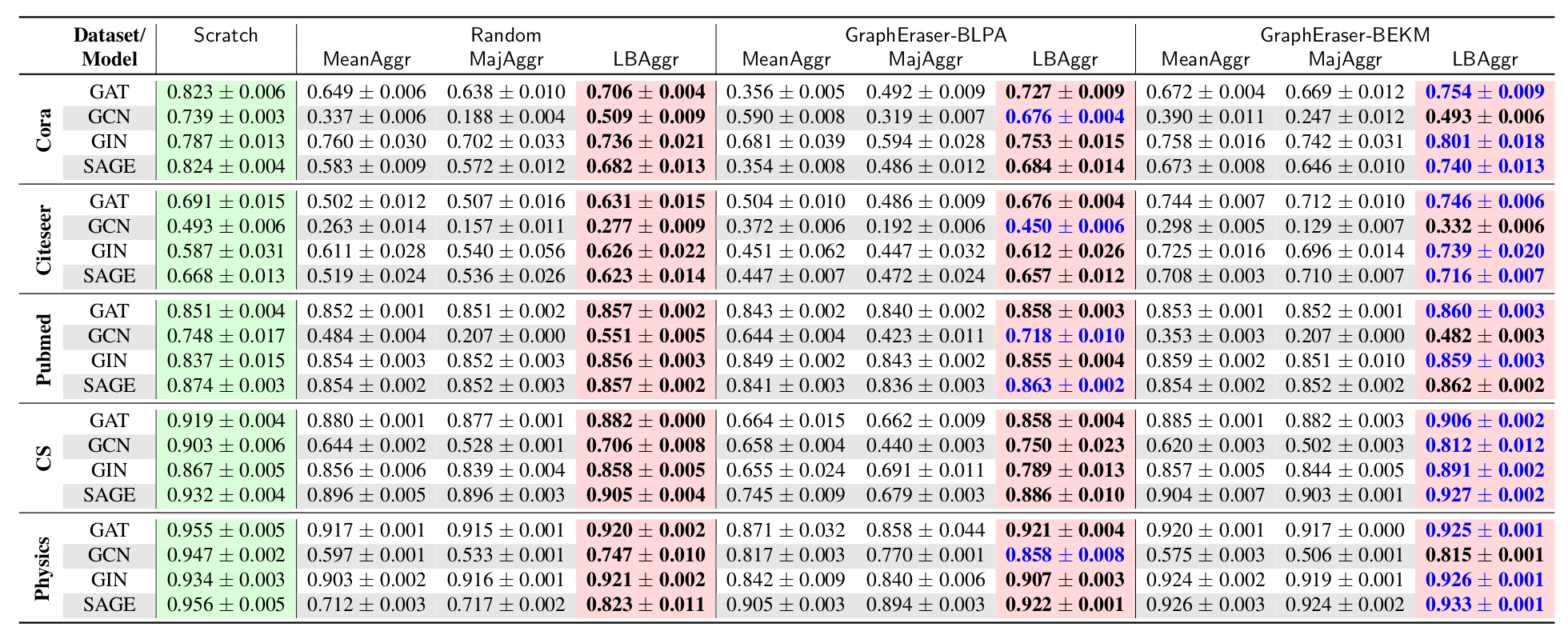
绿色底色表示不需要聚合，红色底色表示作者提出的方法，蓝色字体表示最优得分。

有些随机得分和BLPA和BEKM差不多，作者认为这时由于图结构信息在GNN模型中作用不大导致的。

对此，作者提出了一个方法选择的技巧：可以首先比较MLP和GNN的F1分数，如果MLP和GNN之间的F1分数差距很小，随机方法可能是一个不错的选择，因为它更容易实现，并且可以实现与BLPA和BEKM相当的模型效用。否则，BLPA和BEKM是更好的选择，因为更好的模型实用程序。

如果 GNN 遵循 GCN 结构，则可以选择BLPA，否则可以采用 BEKM。这是因为 GCN 模型需要节点度信息来进行归一化，而BLPA 可以保留更多的局部结构信息，从而更好地保留节点度。

BEKM 在 Cora 数据集和 GIN 模型上的 F1 得分为 0.801，而 Scratch 的相应 F1 得分为 0.787。作者认为有两种可能的原因：抽样往往可以消除数据集中的一些“噪声”；其次，GraphEraser通过聚合所有子模型的结果来进行最终预测，从这个意义上说，GraphEraser执行集成，这是提高模型性能的另一种方法。

# LBAggr 的效果

有效，可以提升F1分数。

比较不同的GNN模型，GCN从LBAggr中受益最大，而GIN受益最少。在模型效用方面，GraphEraser-BLPA方法从LBAggr中受益最大。我们推测这是因为BLPA划分方法可以捕获局部结构信息，同时丢失训练图的一些全局结构信息。

为了进一步提高忘却效率，可以使用训练图中的一小部分节点来学习重要性分数。这样做可以有效地减少 LBAggr 的遗忘学习时间。使用 10% 的节点和使用固定数量的 1，000 个节点都可以实现与使用所有节点相当的模型效用。

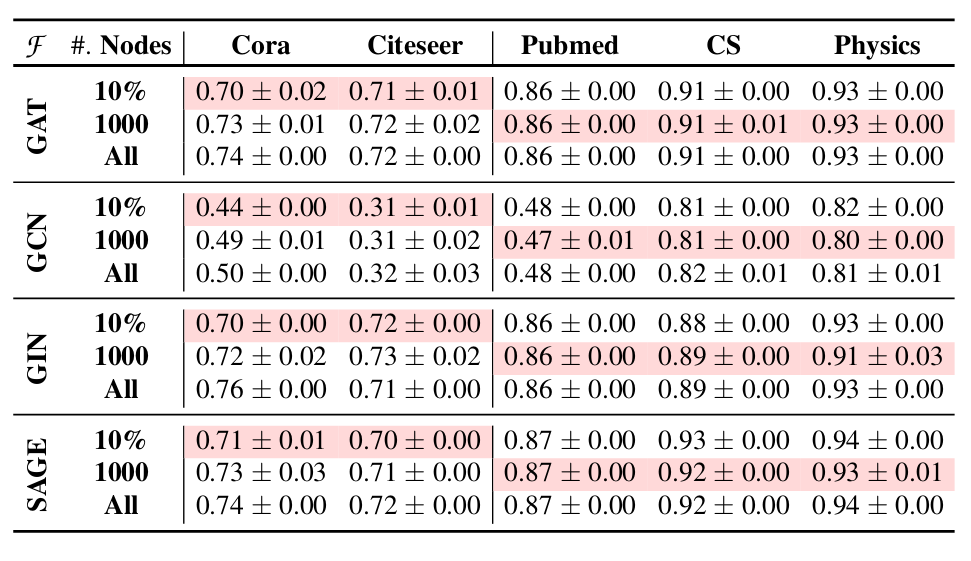
# 和其他遗忘学习方法对比

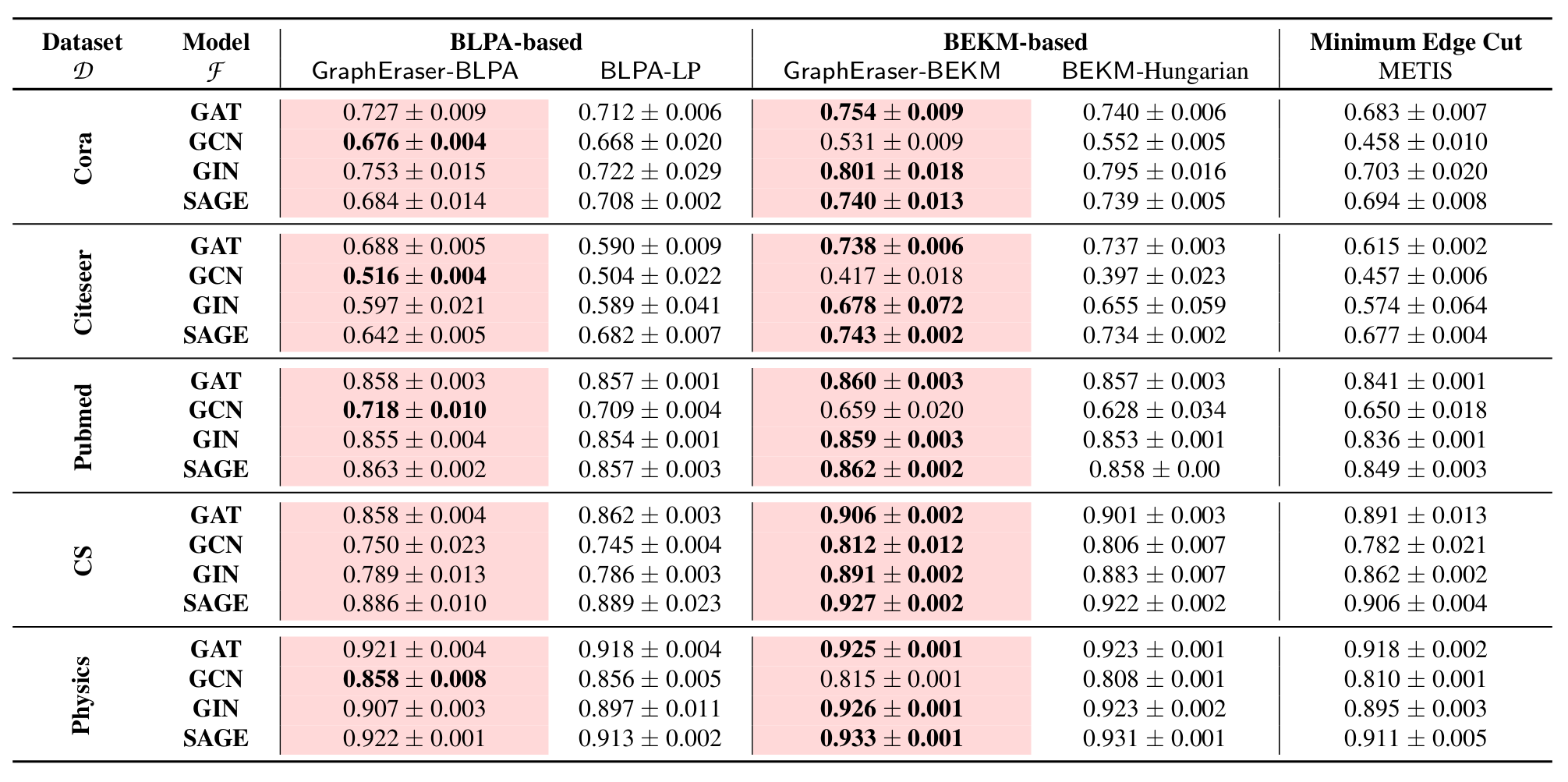
同样，也是作者的方法比较好。