介绍
近年来,人们对利用来自多个组织的分布式源的数据来设计复杂的机器学习模型越来越感兴趣。
但是,由于
- 用户敏感数据的使用被迫遵守标准隐私规章或法律,例如GDPR或CCPA
- 数据是组织保持业务竞争优势的宝贵资产,应该受到高度保护
这两个原因,专有数据不能被直接共享。于是,联邦学习便被提出。联邦学习是一种新兴的数据协作范例,它允许多个数据所有者联合构建ML模型而不向彼此泄露其私有数据。
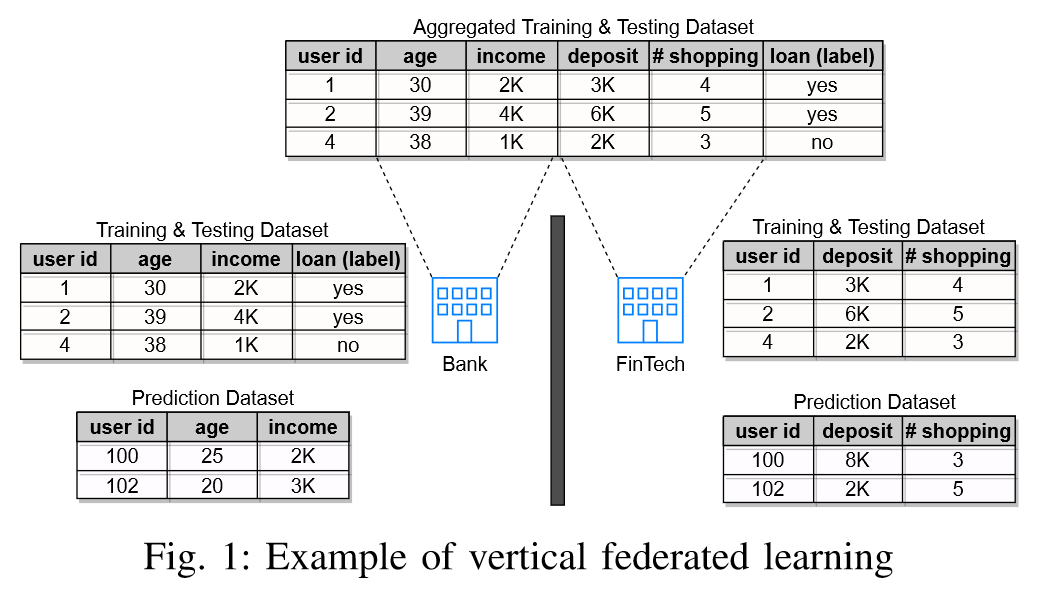
联邦学习根据数据划分,被分为横向联邦学习、纵向联邦学习、联邦迁移学习三类。在本文中,作者主要考虑的是纵向联邦学习这一类。何为纵向联邦学习呢?也就是2个数据集的用户重叠部分较大,而用户特征重叠部分较小,作者给出了一个实例:
一家银行希望构建一个机器学习模型,通过加入Fintech公司的更多特性来评估是否批准用户的信用卡申请。这家银行拥有“年龄”和“收入”的特征,而Fintech公司拥有“存款”和“平均在线购物次数”的特征。只有银行拥有训练数据集和测试数据集中的标签信息,即:是否应批准申请。我们将带有标签的一方称为主动方,其余没有标签值的一方或者几方称为被动方。
在本篇文章中,把拥有标签值的一方看作进攻方,而没有标签值的一方或者几方所拥有的特征值看作目标值,进攻方通过一定的方法得到目标方的目标值,也就是通常模型中被动方的隐私数据。
相关研究
- Comprehensive privacy analysis of deep learning: Stand-alone and federated learning under passive and active white-box inference attacks
- The secret sharer: Measuring unintended neural network memorization & extracting secrets
- Exploiting unintended feature leakage in collaborative learning
- Deep models under the gan: information leakage from collaborative deep learning
等等,这些文章旨在推断横向联邦学习中参与方的特征值,其中各方具有相同的特征但具有不同的样本。 然而,这些攻击极大地依赖于在训练过程中交换的模型梯度,一旦模型梯度被安全地保护,这些攻击将是无效的。而且,对于预测阶段中的推理攻击,联邦学习模型事先不知道预测样本。于是,作者提出几种基于模型预测的特征推理攻击,研究了纵向联邦学习预测阶段的隐私泄露问题,该攻击方法在预测输出的计算过程中不依赖任何中间信息。
本文贡献
- 首次提出了纵向联邦学习预测模型的特征推理攻击
- 提出了针对逻辑回归和决策树的两种特定的攻击思路
- 利用攻方积累的多种预测输出,来设计一种从中学习攻方特征和目标特征关联的通用攻击思路
- 在真实和合成的数据集上,实践了提出的方法并进行了大量的评估。结论显示了攻击的有效性,本文也分析和建议了几种潜在的应对思路
问题构造
系统模型
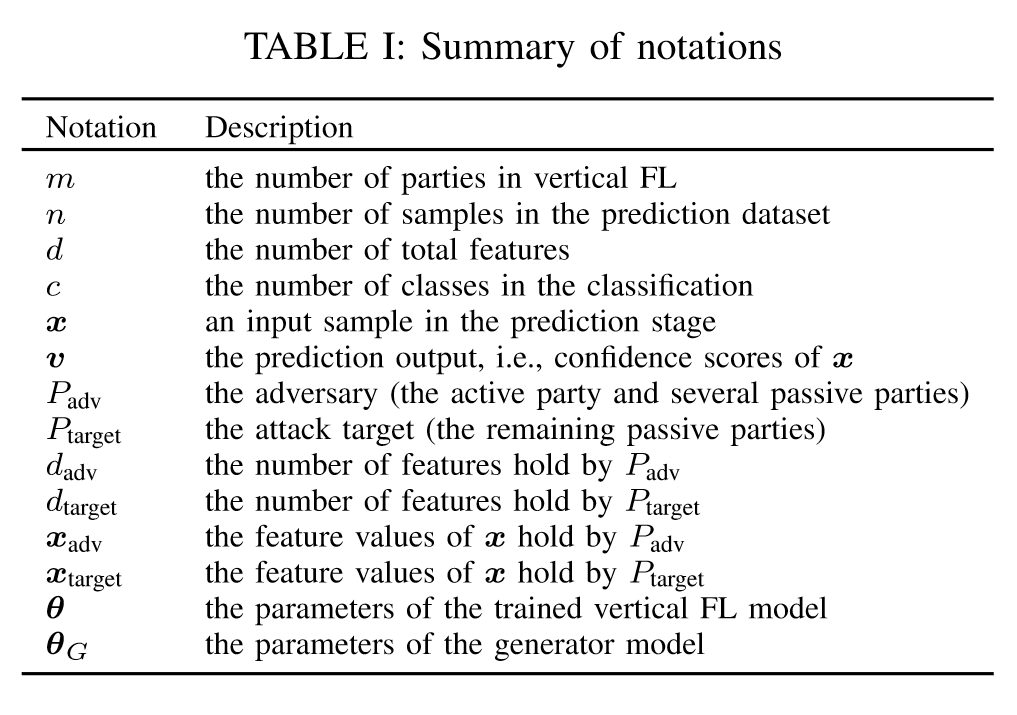
我们考虑一组m个分布方(或数据所有者)${P_1,…,P_m}$,他们通过合并各自的数据集来训练纵向联邦学习模型。在获得经训练的纵向联邦学习模型参数$\theta$之后,各方协作地对其联合预测数据集$D_{pred}={D_1,…,D_m}$进行预测。 数据集中的每一行对应一个样本,每一列对应一个要素。 设$n$为样本数,$d_i$为$D_i$中的特征数,其中$i\in{1,…,m}$。我们表示$D_i={x^t_i}^n_{t=1}$,其中$x^t_i$表示$D_i$的第t个样本。在这篇文章中,作者考虑监督分类任务,并用$c$表示分类的数量。
威胁模型
我们考虑半诚实模型,其中每一方都严格按照规定遵循协议,但可能试图基于接收到的消息推断其他方的私有信息。具体而言,本文着重研究了主动方为对抗方的情形。主动方还可以与其他被动方串通来推断一组目标被动方的私有特征值。最强的概念是m-1个参与方(包括主动方)合谋推断其余被动方的特征值。
攻击方法
逻辑回归模型(LR)的等式求解攻击
给定预测输出$v$,对手$P_{adv}$可以构造一组方程,$P_{adv}$可以从该组方程推断出$P_{target}$所持有的特征值。也就是说攻击者利用纵向联邦学习预测结果以及自己所持有的参数推断数据其他提供方的参数。
作者分别讨论了二分类逻辑回归以及多分类逻辑回归。
二分类逻辑回归
将模型参数表示为$\theta = \theta (\theta_{adv},\theta_{target})$,其中$\theta_{adv}$和$\theta_{target}$分别是对应于$P_{adv}$和$P_{target}$所拥有的特征的权重。
令$v$为给定样本$x=(x_{adv},x_{target})$的预测输出。对于二元LR分类,$v$中只有一个有意义的置信度分数,我们令其为$v_1$。
给定$v_1$和对手自己的特征值$x_{adv}$,$P_{adv}$可以直接创建以$x_{target}$作为变量的方程,即,
$$\sigma\left(x\_{\text {adv }} \cdot \theta\_{\text {adv }}+x\_{\text {target }} \cdot \theta\_{\text {target }}\right)=v\_{1}$$其中$\sigma(\cdot)$是S形函数。显然,如果只有一个未知特征,即,$d_{target} = 1$,则方程只有一个解,这意味着可以精确地推断未知特征值$x_{target}$。
多分类逻辑回归
对于多分类逻辑回归,存在$c$个线性回归模型。设$\theta = (\theta^{(1)},…,\theta^{(c)})$分别为这些$c$模型的参数。
为了发起特征推理攻击,对手的目标是构造$k\in{1,…,c}$的线性方程。
$$x \_ { a d v } \cdot \theta \_ { a d v } ^ { ( k ) } + x \_ { target } \cdot \theta \_ { target } ^ { ( k ) } = z \_ { k }$$其中$z_k$是第$k$个线性回归模型的输出。然而,$P_{adv}$只知道置信度向量$v =(v_1,…,v_c)$,使得
$$v \_ { k } = \frac { e x p ( z \_ { k } ) } { \sum \_ { k' } exp ( z \_ { k' } ) }$$上面两个式子是我们用逻辑回归解决多分类问题的通用的公式,其中作者在第一个式子中把x和θ分成了攻方和目标方的数据。
作者将第二个式子双方取对数
$$\ln v \_ { k } = z \_ { k } - \ln ( \sum \_ { k ^ { \prime } } e x p ( z \_ { k } ^ { \prime } ) )$$等式右边的第二项对于所有$k\in{1,…,c}$是相同的。因此,对两个相邻类别概率v的对数取差值
$$\ln v \_ { k } - \ln v \_ { k'} = z \_ { k } - z \_ { k' }$$最后可以得到一个无关z值的一个等式
$$x\_{\text {adv }}\left(\theta\_{\text {adv }}^{(k)}-\theta\_{\text {adv }}^{(k+1)}\right)+x\_{\text {target }}\left(\theta\_{\text {target }}^{(k)}-\theta\_{\text {target }}^{(k+1)}\right)=a\_{k}^{\prime}$$其中$a^\prime_k=\ln v_k-\ln v_{k+1},k\in{1,…,c}$。
但是在后面推理的时候本文有一些为了逻辑上方便而采用了一个把纵向联邦限制减少的做法:把目标方或者说被动方的参数θ看作进攻方或者主动方能够得到的数据。
实际情况中,主动方或者进攻方在一般的纵向联邦框架中是无法得到被动方的参数θ数据的。
本文中我们姑且认为进攻方能得到,那么上式中的未知数只有$x_{target}$了,而$x_{target}$的维数为$d_{target}$,数量为目标方所用拥有的特征数。
这里我们把$x_{target}$的未知数看作自变量,个数为目标放所拥有的特征数。那么也就是说,$d_{target}$个自变量,$c-1$个方程,当$d_{target}\le c-1$,那么$x_{target}$只有一个解,可以精确地推断出来。
决策树模型的路径限制攻击
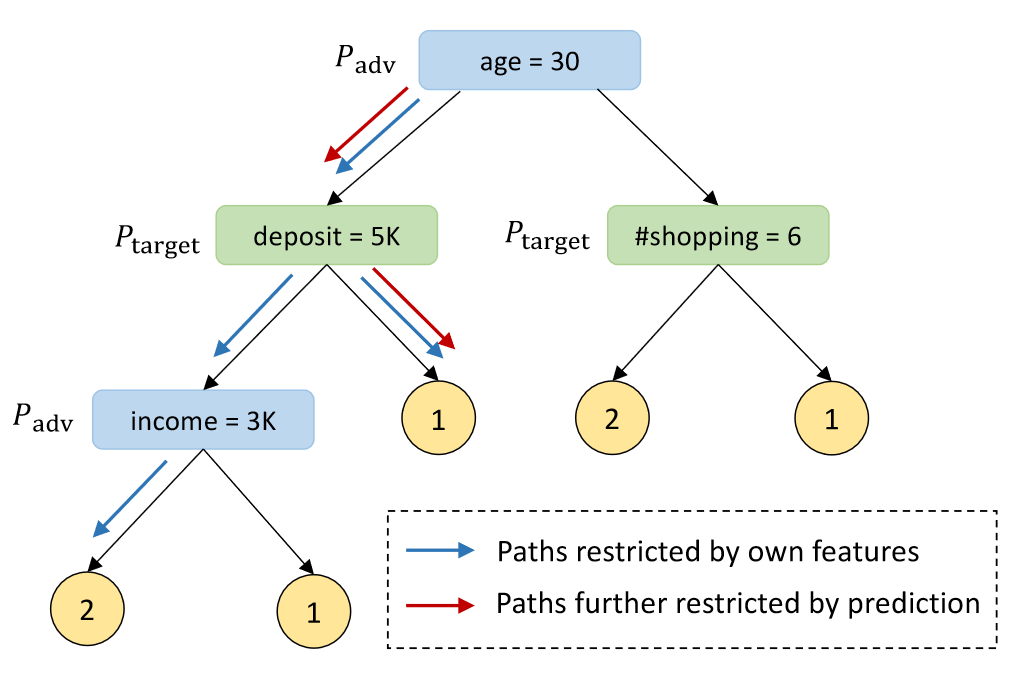
攻击方可以根据自己的部分特征信息(蓝色方框) 限制树模型中可能的路径(灰色箭头 -> 蓝色箭头 5:2),结合预测类别结果1进一步限制决策路径(蓝色 - > 红色箭头 2:1 ),可以推测目标方Target的deposit属性(绿色方框) > 5K。

生成回归网络攻击
上面介绍的两种攻击方式都是基于单个模型预测。然而,这些攻击很难应用于复杂的模型,如神经网络(NN)和随机森林(RF)。
针对上述缺陷,作者设计了一种基于多模型预测的通用特征推理攻击,即生成回归网络(GRN)攻击,这是本篇论文的重点。
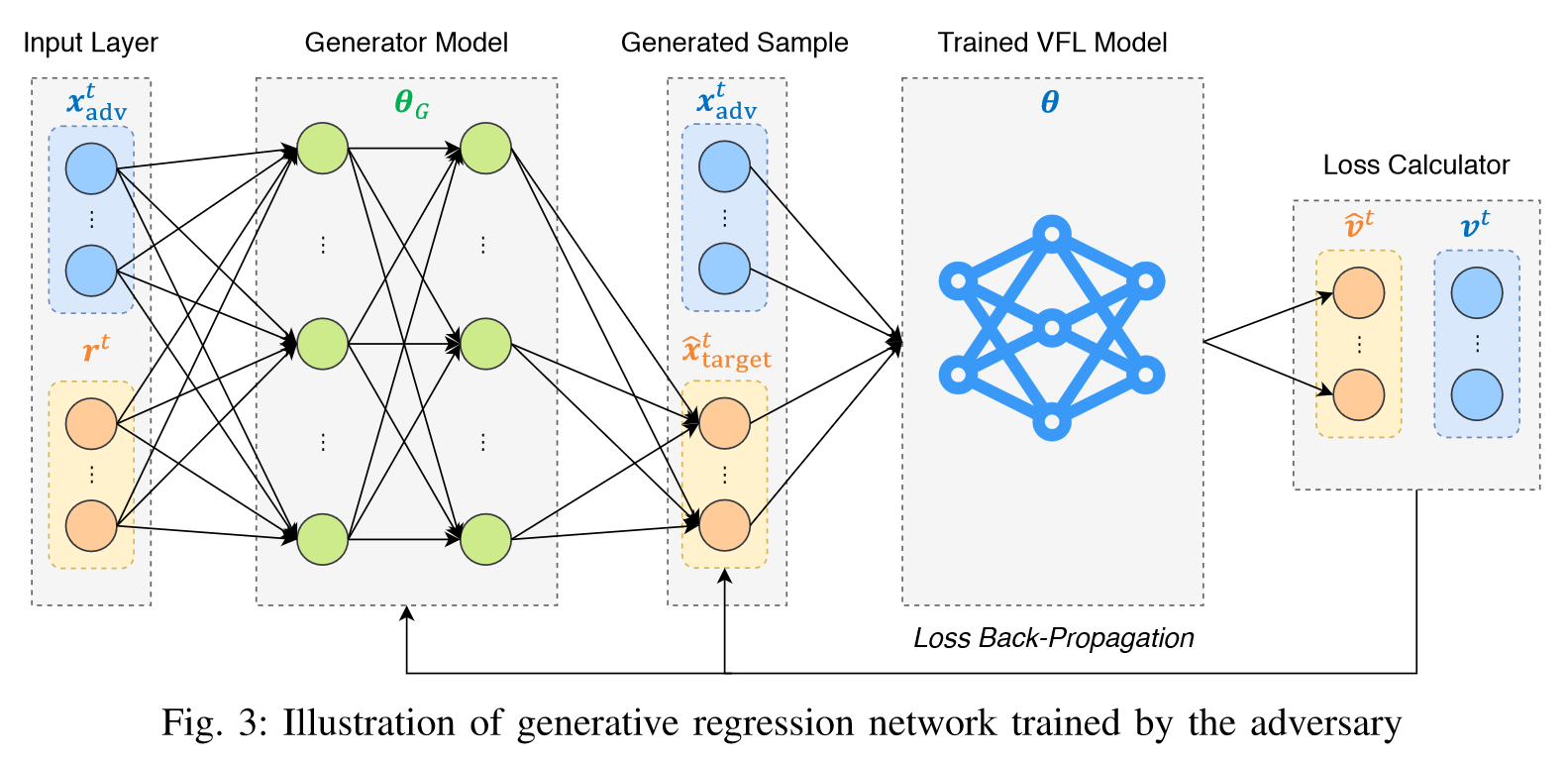
基本思想:
计算出对手自身特征与攻击目标未知特征之间的总体相关性。在此基础上,推断未知特征值的问题等效于生成新值$\hat{x}_{target}$以匹配垂直FL模型的决策的问题,其中$\hat{x}_{target}$遵循由对手的已知特征值和特征相关性确定的概率分布。
目标函数:
$$\min \_{\theta\_{G}} \frac{1}{n} \sum\_{t=1}^{n} \ell\left(f\left(x\_{\mathrm{adv}}^{t}, f\_{G}\left(x\_{\mathrm{adv}}^{t}, r^{t} ; \theta\_{G}\right) ; \theta\right), v^{t}\right)+\Omega\left(f\_{G}\right)$$其中$\theta$和$\theta_G$分别是纵向联邦学习模型和生成模型的参数。此外,$f_G$表示$\hat{x}_{target}^t$,即生成模型的输出,$f$表示给定所生成样本的纵向联邦学习模型的输出(由$x_{adv}^t$和$\hat{x}_{target}^t$连接)。此外,$\Omega(\cdot)$是生成的未知特征值${\hat{x}_{target}^t}_{t=1}^n$的正则化项。
具体方法:
把进攻方所拥有的数据(蓝色)和随机生成的数据(橙色),合成一个d维向量,其中d为进攻方的特征数量和目标方特征数量之和,随机生成的数据是为了初始化生成模型的初始输入。
生成模型计算之后,输出生成模型对于目标方特征值的预测。
把生成模型生成的目标方特征值的预测(橙色)与进攻方所拥有的数据(蓝色)合并,得到另一个d维的向量,作为已经生成的纵向联邦学习预测模型(比如神经网络)的输入。
得到输出的对不同类别的预测概率矩阵(橙色),与真实的攻方特征值和目标方特征值得到的不同类别的预测概率矩阵(蓝色)求损失。
对得到的损失进行反向传播,修改生成模型的参数,得到新的生成模型对目标放特征值的预测。
这种方法对于目标函数为可微的情况下效果不错,也就说明可以用来对逻辑回归和神经网络进行生成模型攻击。

随机森林的生成模型的攻击
路径限制攻击不适用于随机森林的模型,特别是当随机森林的树数量很大的时候。
因此,在随机森林模型使用GRN攻击的思想。
但是,因为随机森林(RF)模型的目标函数并不是可微的,所以不能通过随机森林(RF)把预测损失反向传播给生成模型。
因此,本文在得到纵向联邦模型(比如随机森林RF)之后,攻方会另外训练一个可微的模型(比如神经网络NN)来近似RF模型。
实验评价
数据集:
四个数据集,分别是银行营销(20个特征的2分类),信用卡(23个特征的2分类),诊断(48个特征的11分类)和新闻流行(59个特征的5分类)。
此外,利用sklearn库生成了两个合成数据集,用于评估预测数据集中样本数n对生成回归网络攻击性能的影响。
指标:
对于等式求解攻击(ESA)和生成回归网络攻击(GRNA),由于是回归任务,因此使用每个特征的均方误差(MSE)来衡量它们在重建多个目标特征时的总体准确性。具体而言,每个特征的MSE计算如下:
$$\mathrm{MSE}=\frac{1}{n * d\_{\text {target }}} \sum\_{t=1}^{n} \sum\_{i=1}^{d\_{\text {target }}}\left(\hat{x}\_{\text {target }, i}^{t}-x\_{\text {target }, i}^{t}\right)^{2}$$对于路径限制攻击(PRA),作者测量了正确分支率(CBR)。
$d_{target}$对等式求解攻击的影响
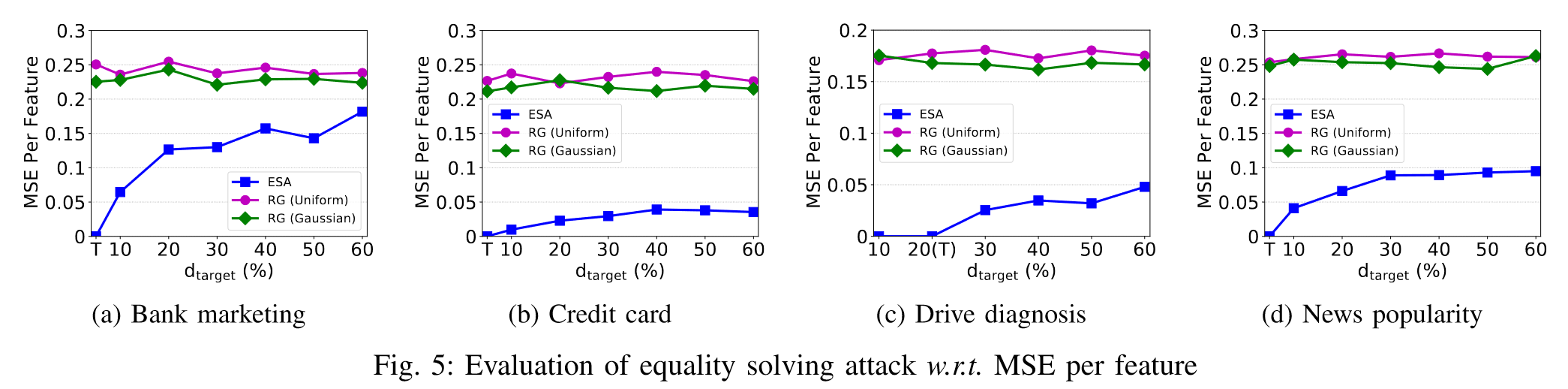
对于所有数据集,如果满足阈值条件$d_{target}\le c-1$(在每个子图中用“T”表示),则每个特征的MSE为0,这证明了上面讨论的性质正确。
通过观察b和c,我们发现即使不满足阈值条件,等式求解攻击仍然可以找到$x_{target}$的良好推断,这大大优于随机猜测方法。
还有一个明显的趋势,每个特征的MSE随着$d_{target}$分数的增加而增加,即攻方所掌握的特征数越少,供给的准确率越低。
同时,作者还分析了为什么Bank数据集的MSE增量远大于其他数据集的MSE增量,这是因为不同数据集的数据分布差异。
由伪逆矩阵计算出的解$\hat{x}_{target}$在所有解中具有最小的欧几里德范数,即$||\hat{x}_{target}||_2\le||x_{target}||_2$
其中
$$\sum\_{i=1}^{d\_{\text {target }}} \hat{x}\_{\text {target }, i}^{2} \leq \sum\_{i=1}^{d\_{\text {target }}} x\_{\text {target }, i}^{2}$$因此,我们有
$$\begin{aligned} \mathrm{MSE} & =\frac{1}{d\_{\text {target }}} \sum\_{i=1}^{d\_{\text {target }}}\left(\hat{x}\_{\text {target }, i}-x\_{\text {target }, i}\right)^{2} \\\\ & =\frac{1}{d\_{\text {target }}} \sum\_{i=1}^{d\_{\text {target }}}\left(\hat{x}\_{\text {target }, i}^{2}+x\_{\text {target }, i}^{2}-2 \hat{x}\_{\text {target }, i} x\_{\text {target }, i}\right) \\\\ & \leq \frac{1}{d\_{\text {target }}} \sum\_{i=1}^{d\_{\text {target }}}\left(\hat{x}\_{\text {target }, i}^{2}+x\_{\text {target }, i}^{2}\right) \\\\ & \leq \frac{1}{d\_{\text {target }}} \sum\_{i=1}^{d\_{\text {target }}} 2 x\_{\text {target }, i}^{2}, \end{aligned}$$我们便推导出$\mathrm{MSE}(\hat{x}_{target},x_{target})$的上界。
作者分别计算了Bank、Credit、Drive和News四个数据集的上界,分别为0.60、0.14、0.45和0.34。
一般来说,上界越大,对手的攻击精度就越差。这就解释了为什么Bank的MSE比其他数据集增长得更快。
$d_{target}$对路径限制攻击的影响
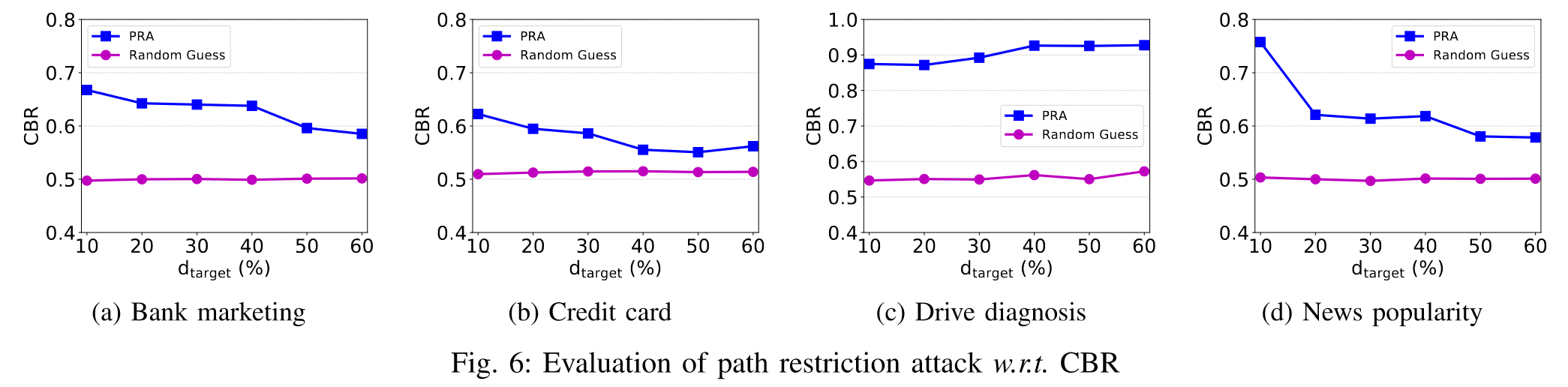
与等式求解攻击类似,攻击精度随着$d_{target}$的增加而降低。这是因为通常更多的目标特征将导致更多可能的预测路径,从而导致选择正确路径的概率降低。
我们可以发现,第三个数据集是异常的,它甚至随着$d_{target}$的增加而增加了。这是因为Drive数据集有11个类,比其他数据集的类要多得多。因此,在Drive中,每个类别对应的树形路径数量较少。其次,决策树模型在训练过程中只选择信息量大的特征,这意味着Drive数据集中$d_{target}$的增加不一定会增加树中未知特征的数量,因为有些特征可能永远不会被选中。
综上,较大的目标数据并不总是能降低路径限制攻击的CBR。
$d_{target}$对生成回归网络攻击的影响
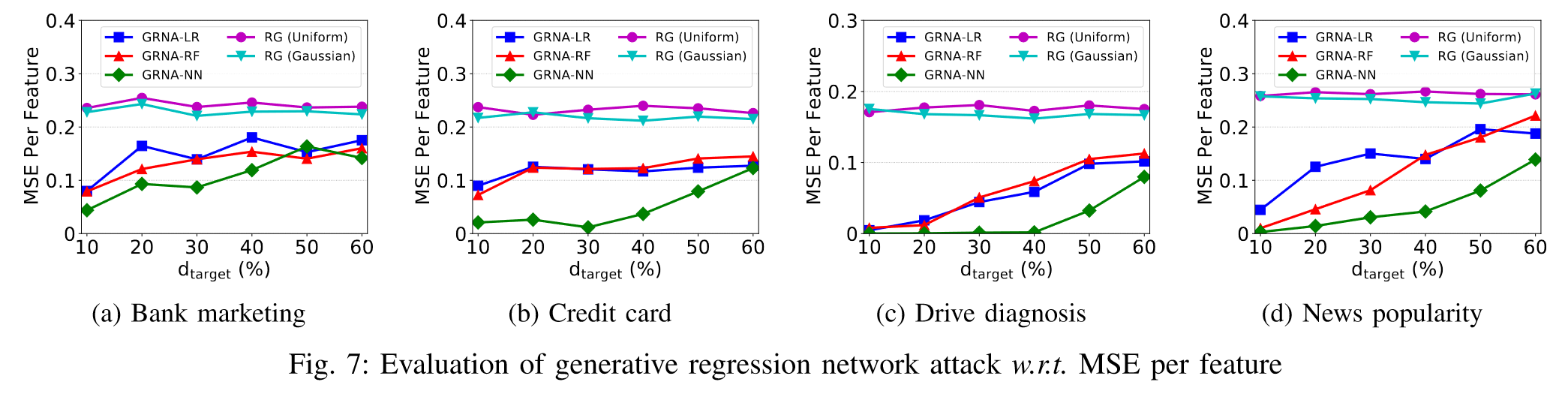
作者展示了生成回归网络攻击对三种模型的攻击性能(LR:逻辑回归、RF:随机森林、NN:神经网络)
类似地,每个特征的MSE都随着$d_{target}$的增加而上升。这是因为生成回归网络攻击依赖于$x_{adv}$和$x_{target}$之间的特征相关性来推断未知特征值。如果$d_{target}$所占比例较大,学习到的相关性会变弱,导致攻击性能相对较差。然而,即使在$d_{target}$的分数为60%时,生成回归网络攻击仍然比随机猜测方法获得了更好的效果,证明了其有效性。
作者发现,采用神经网络模型的生成回归网络攻击的性能优于逻辑回归和随机森林模型。原因在于神经网络模型比其他两种模型具有更复杂的决策边界,从而极大地限制了给定相同$x_{adv}$和$v$时$x_{target}$的可能分布。同时,神经网络模型本身具有更多的参数,可以捕获更多关于特征相关性的重要信息,从而获得更好的攻击性能。
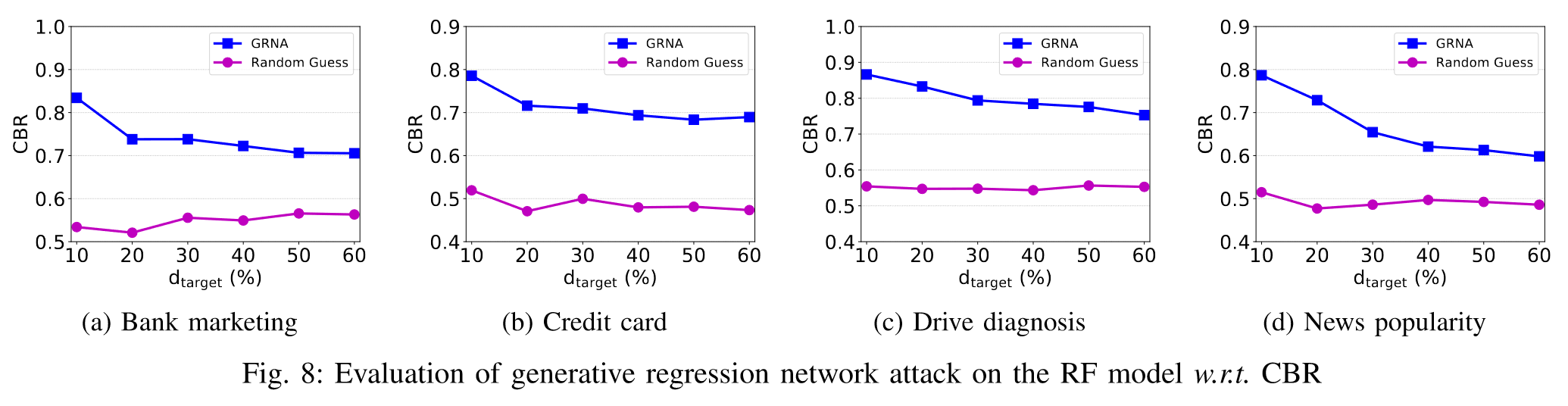
作者还将CBR度量用于评估RF模型上的GRNA,同样效果也比随机猜测方法优秀。
需要预测的样本数对生成回归网络攻击的影响
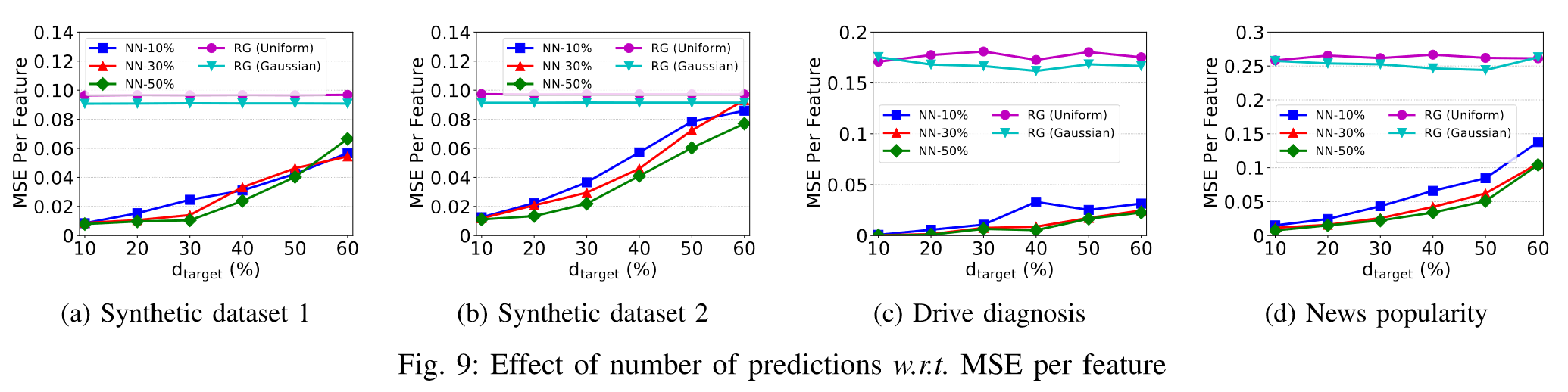
四个数据集上的趋势表明,预测数据集中的样本越多,对手可以获得的每个特征的MSE越少。 换句话说,对手可以长期积累更多的预测输出,以提高其攻击精度。
数据相关性对生成回归网络攻击的影响
由于LR和RF模型的性能低于NN模型,作者推断是因为一小部分推断出的特征值与真实相差甚远,导致整体攻击性能相对较低,于是作者研究数据相关性的影响。
数据相关性定义如下:
$$\begin{aligned} \operatorname{corr}\left(x\_{\mathrm{adv}}, x\_{\mathrm{target}, i}\right) & =\frac{1}{d\_{\mathrm{adv}}} \sum\_{j=1}^{d\_{\mathrm{adv}}} a b s\left(r\left(x\_{\mathrm{adv}, j}, x\_{\mathrm{target}, i}\right)\right), \\\\ \operatorname{corr}\left(v, x\_{\mathrm{target}, i}\right) & =\frac{1}{c} \sum\_{j=1}^{c} a b s\left(r\left(v\_{j}, x\_{\mathrm{target}, i}\right)\right), \end{aligned}$$其中$r(a,b)$表示a和b之间的皮尔逊相关系数,$abs(\cdot)$表示绝对值。 本质上,两个系数越大,对手越容易通过生成回归网络攻击学习特征相关性。
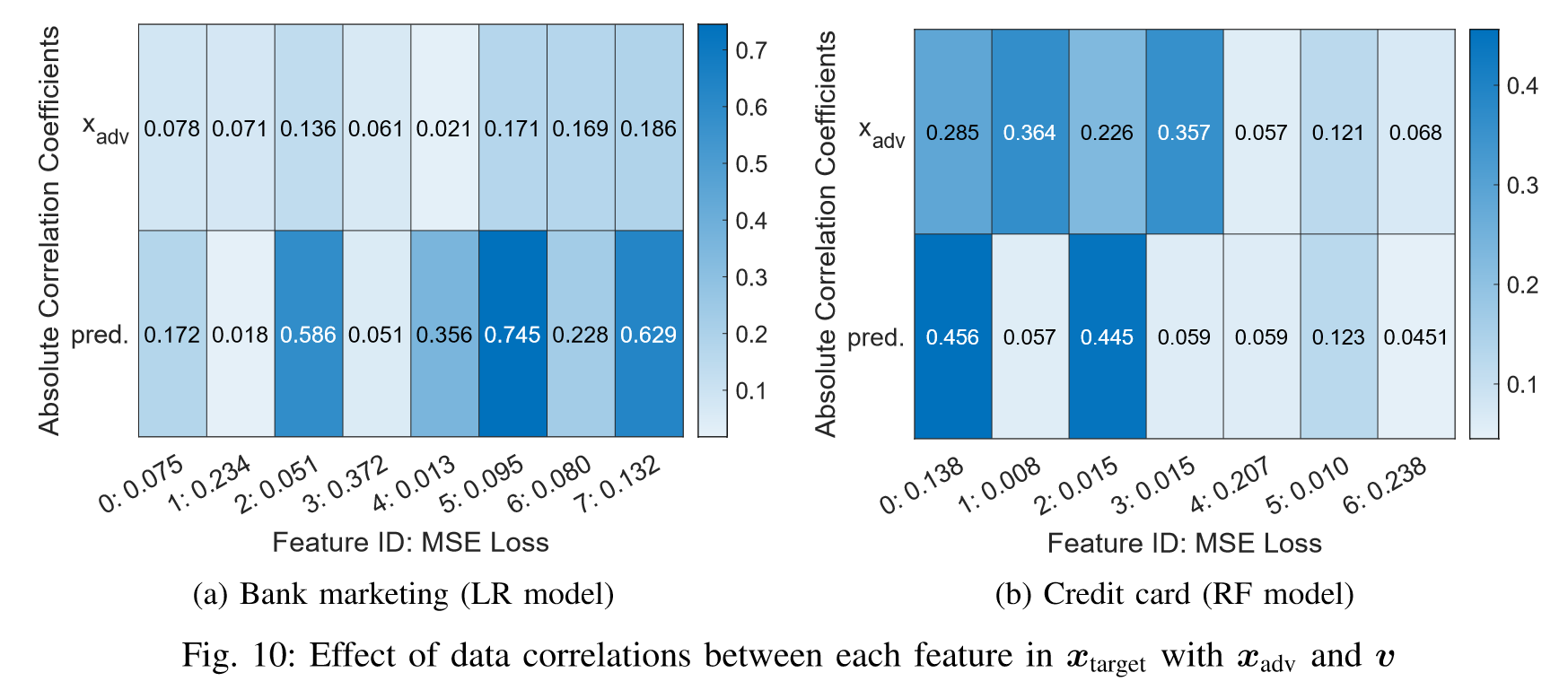
我们可以观察到相关系数$x_{adv}$和$v$都会影响生成回归网络攻击的攻击性能。$x_{target}$,$i$与$x_{adv}$和$v$之间较弱的相关性导致较低的推断准确度,例如图10a中的特征1和3以及图10b中的特征4和6。
对策
作者讨论了几种可能减轻所提出的特征推断攻击的潜在防御方法。
| 策略名称 | 效果 |
|---|---|
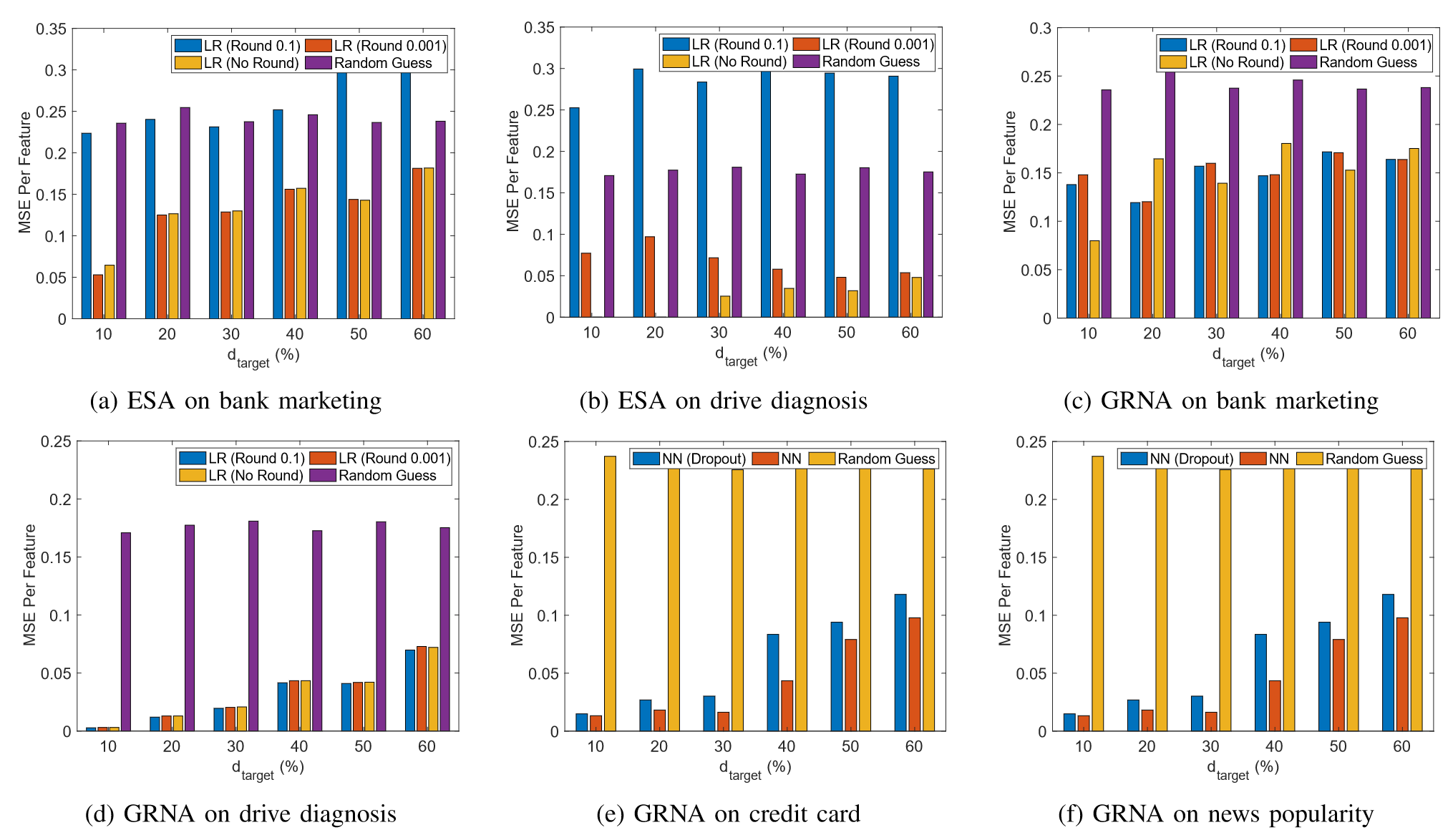
| Rounding confidence scores | 等式求解攻击有效,但生成回归网络攻击效果甚微 |
| Dropout for neural networks model | 有效,但攻击者还是有一个很好的推断 |
| Pre-processing before collaboration | 未做测试 |
| Post-processing for verification | 导致模型预测计算的巨大开销 |
| Hide the vertical FL model | 可能会导致新的隐私泄露 |
| Differential Privacy (DP) | 不适用 |
