# 介绍

最近的研究表明，深度神经网络 （DNN） 容易受到后门攻击，攻击者通过毒害一些训练数据将隐蔽的后门注入 DNN。具体来说，后门攻击者将后门触发器（即特定模式）附加到一些良性训练数据，并将其标签更改为攻击者指定的目标标签。触发模式和目标标签之间的相关性将由 DNN 在训练期间学习。在推理过程中，后门模型在良性数据上表现正常，而当后门被激活时，其预测会被恶意改变。

相反，人类认知系统能够抵抗输入的扰动，例如后门攻击引起的隐蔽触发模式。这是因为人类对因果关系的敏感度高于干扰因素的关联。相比之下，经过训练以拟合中毒数据集的深度学习模型很难区分后门攻击带来的因果关系和统计关联。通过因果推理，我们可以识别因果关系并建立鲁棒的深度学习模型。因此，必须利用因果推理来分析和减轻后门攻击的威胁。

那么。什么是因果推理呢？因果推断在统计研究中有着悠久的历史。因果推理的目标是分析变量之间的因果效应，并减轻虚假相关性。

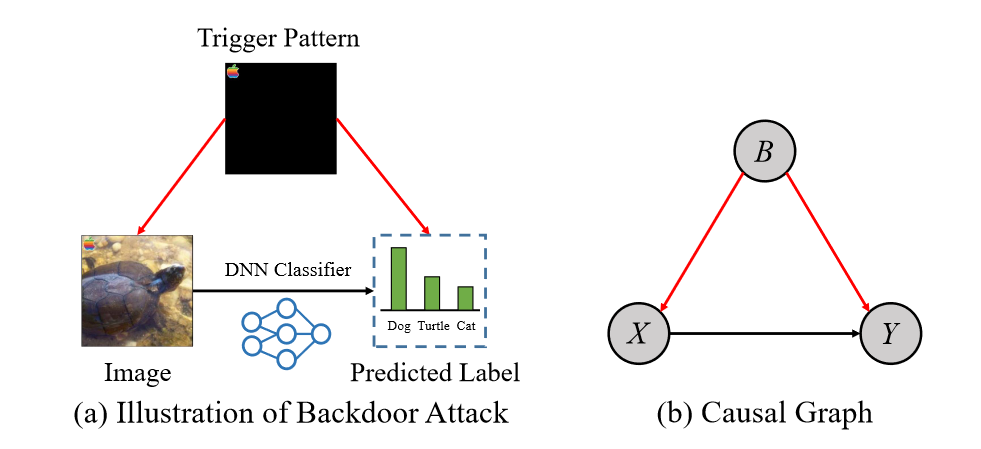
作者专注于图像分类任务，目标是在没有额外干净数据的情况下，在含有毒数据的数据集上训练出无后门的模型。作者首先构建了一个因果图来模拟后门数据的生成过程，特别考虑了干扰因素，即后门触发模式。借助因果图，发现后门攻击扮演了混杂因素的角色，并在输入图像与预测标签之间建立了一条虚假的联系。一旦深度神经网络学习了这种虚假联系，当附加了触发器时，它们的预测就会发生改变，转向目标标签。

作者在因果洞察的启发下，提出了一种新的后门防御方法，称为因果关系启发的后门防御（Causalityinspired Backdoor Defense，CBD），旨在学习去混淆的分类表示。由于后门攻击隐蔽且难以直接测量，无法通过因果推理直接阻断后门路径。受到解缠绕表征学习最新进展的启发，作者的目标是学习一种表征，它只保留与因果关系相关的信息。在CBD中，作者训练了两个深度神经网络（DNN）：一个专注于捕获虚假相关性，另一个专注于识别因果效应。第一个DNN通过提前停止策略有意地学习后门相关性。接着，我们通过最小化互信息训练第二个干净的模型，使其在隐藏空间中独立于第一个模型。训练完成后，只有干净的模型被用于下游的分类任务。

# 问题构造

作者假设攻击者已经预先生成了一组后门示例，并成功地将它们注入到训练数据集中。同时，作者假设防御者能够完全控制训练过程，但对数据集中后门示例的分布或比例一无所知。防御者的目标是训练出一个在中毒数据集上表现良好且无后门的模型，其性能应与在纯干净数据上训练的模型相当。一句话总结，就是在后门数据集上训练出一个干净模型。

# 因果分析

因果推理的优越性在于它使人类能够识别因果关系，同时忽略任务中的非必要因素。相比之下，深度神经网络通常无法区分因果关系和统计关联，并且倾向于学习那些“更容易”的相关性，而不是必要的信息。这种走捷径的解决方案可能导致对无关因素（例如触发模式）的过度拟合，从而增加了后门攻击的脆弱性。因此，作者利用因果推理来分析DNN模型的训练过程，并降低后门注入的风险。

作者通过构建因果图$G$来模拟中毒数据的生成过程。在因果图中，作者使用节点来表示抽象数据变量，其中$X$代表输入图像，$Y$代表标签，$B$代表后门攻击。有向链接则表示这些变量之间的关系。除了$X$对$Y$的因果效应（$X → Y$）之外，后门攻击者可以通过将触发模式附加到图像（$B → X$）并将标签更改为目标标签（$B → Y$）来实施攻击。因此，后门攻击 $B$ 作为 $X$ 和 $Y$ 之间的混杂因素，打开了虚假路径 $X ← B → Y$（其中 $B = 1$ 表示图像中毒，$B = 0$ 表示图像干净）。我们所说的“虚假”路径是指这条路径位于 $X$ 到 $Y$ 的直接因果路径之外，它使得 $X$ 和 $Y$ 之间产生了虚假的相关性，并在触发器被激活时导致错误的效果。深度神经网络（DNN）很难区分虚假相关性和因果关系。因此，如果在可能中毒的数据集上直接训练 DNN，模型将面临被后门攻击的风险。

为了探究 $X$ 对 $Y$ 的因果效应，研究者通常使用 do 演算在因果干预中进行后门调整：$P(Y|do(X)) = \sum_{B\in\{0,1\}}P(Y|X,B)P(B)$。然而，在作者的设置中，由于混杂变量 $B$ 几乎无法被检测和测量，不能简单地使用后门调整来阻断后门路径。相反，由于大多数深度学习模型的目标是学习下游任务的准确嵌入表示，所以目标是解开隐藏空间中的混淆效应和因果效应。

# 基于因果推理的后门防御

在现实应用中，直接识别数据空间中 $X$ 的混杂因素和因果因素可能相当困难。作者假设这些混杂因素和因果因素会在隐藏的表征中得到体现。通常，训练包括两个 DNN，即 $f_B$ 和 $f_C$，它们分别专注于捕获虚假相关性和因果关系。作者从 $f_B$ 和 $f_C$ 的倒数第二层提取嵌入向量，分别表示为 $R$ 和 $Z$。为了避免混淆，本文中使用大写字母表示变量，小写字母表示具体值。为了生成能够捕获因果关系的高质量变量 $Z$，作者在训练阶段，首先在中毒数据集上训练 $f_B$，以捕捉后门的虚假相关性。随后，训练另一个干净的模型 $f_C$，鼓励其在隐藏空间（即 $Z$ 与 $R$ 独立）中的独立性，并通过最小化互信息和实施样本重新加权策略。训练完成后，只有 $f_C$ 被用于下游的分类任务。

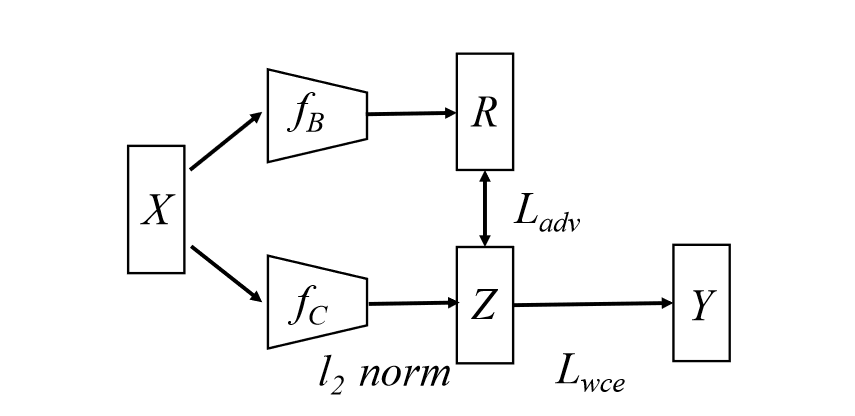
# 后门模型训练

首先，作者在具有交叉熵损失的毒数据集上训练 $f_B$，目的是捕获后门的虚假相关性。由于中毒数据仍然包含因果关系，作者有意通过早期停止策略来增强 $f_B$ 中的混杂偏差。具体来说，作者只对 $f_B$ 进行了少数几个时期的训练（例如，5 个时期），并在训练 $f_C$ 时冻结了其参数。这是因为先前的研究表明，后门关联比因果关系更容易被学习。

# 干净模型训练

作者提出了具有信息瓶颈和互信息最小化的训练目标：

$$\mathcal{L}_C=\min\underbrace{\beta I(Z;X)}_{1}-\underbrace{I(Z;Y)}_{2}+\underbrace{I(Z;R)}_{3}$$

其中$I(.;.)$​表示互信息

• ①用来限制来自输入的不相关信息
• ②用来捕获变量 $Z$​ 用于标签预测的核心信息
• ③描述了后门嵌入 $R$ 和去混淆嵌入 $Z$ 之间的依赖程度。它鼓励 $Z$ 独立于 $R$，通过最小化互信息来关注因果效应

互信息

互信息（mutual Information，MI）度量了两个变量之间相互依赖的程度。具体来说，对于两个随机变量，MI是一个随机变量由于已知另一个随机变量而减少的“信息量”（单位通常为比特）。

$$I(X;Y)=D_{\mathrm{KL}}(p(x,y)|p(x)\otimes p(y))$$

直观上，互信息度量 X 和 Y 共享的信息：它度量知道这两个变量其中一个，对另一个不确定度减少的程度。例如，如果 X 和 Y 相互独立，则知道 X 不对 Y 提供任何信息，反之亦然，所以它们的互信息为零。在另一个极端，如果 X 是 Y 的一个确定性函数，且 Y 也是 X 的一个确定性函数，那么传递的所有信息被 X 和 Y 共享：知道 X 决定 Y 的值，反之亦然。

然而，上述的公式并不能直接求解，为此，作者放宽了限制。

公式1

$$\begin{aligned} I(Z;X)& =\sum_x\sum_zp(z,x)\mathrm{log}\frac{p(z,x)}{p(z)p(x)} \\ &=\sum_x\sum_zp(z|x)p(x)\mathrm{log}\frac{p(z|x)p(x)}{p(z)p(x)} \\ &=\sum_x\sum_zp(z|x)p(x)\mathrm{log~}p(z|x)-\sum_zp(z)\mathrm{log~}p(z) \end{aligned}$$

然而，边际概率$p(z)=\sum_xp(z|x)p(x)$在实践中很难计算，为此作者通过变分分布$q(z)$来近似$p(z)$，由于KL散度是非负的，根据吉布斯不等式：$D_{\mathrm{KL}}(p(z)||q(z)) \geq 0 \Rightarrow -\sum_zp(z)\mathrm{log~}p(z)\leq-\sum_zp(z)\mathrm{log~}q(z)$

将其代入上式：

$$\begin{aligned} I(Z;X)& \leq\sum_xp(x)\sum_zp(z|x)\mathrm{log~}p(z|x)-\sum_zp(z)\mathrm{log~}q(z) \\ &=\sum_xp(x)\sum_zp(z|x)\mathrm{log}\frac{p(z|x)}{q(z)} \\ &=\sum_xp(x)D_{\mathrm{KL}}(p(z|x)||q(z)) \end{aligned}$$

作者假设$p(z|x)=\mathcal{N}(\mu(x),\mathrm{diag}\{\sigma^2(x)\})$是高斯分布，其中$\mu(x)$是$x$的编码嵌入，$\mathrm{diag}\{\sigma^2(x)\}=\{\sigma_d^2\}_{d=1}^D$表示方差的对角矩阵，并假设$q(z)=\mathcal{N}(0,I)$，于是上式就可以改写成：

$$D_{\mathrm{KL}}(p(z|x)||q(z))=\frac{1}{2}||\mu(x)||_2^2+\frac{1}{2}\sum_d(\sigma_d^2-\mathrm{log}\sigma_d^2-1)$$

为了便于优化作者将$\sigma(x)$定义为全零矩阵，所以$z=\mu(x)$成为确定性嵌入。

最后推导出来，公式一就相当于直接在嵌入向量 $z$ 上应用L2正则化

公式2

根据互信息的定义，有$I(Z;Y)=H(Y)-H(Y|Z)$，其中$H(·)$ 和 $H(·|·)$ 分别表示熵和条件熵。由于$H(Y)$ 是一个正常数，可以忽略不计，因此有以下不等式：

$$-I(Z;Y)\leq H(Y|Z)$$

在实验中，$H(Y|Z)$可以计算并优化为交叉熵损失。为了进一步鼓励 $f_C$ 和 $f_B$ 之间的独立性，作者固定了 $f_B$ 的参数，并使用样本加权交叉熵损失来训练 $f_C$，权重的计算公式为：

$$w(x)=\frac{CE(f_B(x),y)}{CE(f_B(x),y)+CE(f_C(x),y)}$$

对于 $f_B$上损失较大的样本，$w(x)$接近1;而当损失非常小时，$w(x)$接近 0。从而让 $f_C$专注于 $f_B$的“难”示例，以鼓励其独立性。

公式3

基于互信息和KL散度的关系，有$I(Z;R)=D_{\mathrm{KL}}(p(Z,R)||p(Z)p(R))$，即$I(Z;R)$等价于联合分布$p(Z,R)$和两个边际$p(Z)p(R)$的乘积之间的KL散度。

为了最小化混杂惩罚项，作者采用了对抗学习。判别器$D_\phi$被训练成将联合分布$p(Z,R)$分类为1，将边际分布$p(Z)p(R)$分类为0。边际分布$p(Z)p(R)$的样本是通过对$p(Z,R)$训练批次中样本$(z,r)$的单个表示进行shuffle而获得的。优化函数如下：

$$\mathcal{L}_{adv}=\min_{\theta_C}\max_\phi\mathbb{E}_{p(z,r)}[D_\phi(z,r)]-\mathbb{E}_{p(z)p(r)}[D_\phi(z,r)]$$

其中$\theta_C$ 和$\phi$分别表示 $f_C$ 和 $D_\phi$ 的参数。

综上，$f_C$的损失函数为：

$$\mathcal{L}_C=\mathcal{L}_{wce}+\mathcal{L}_{adv}+\beta||\mu(x)||_2^2$$​

算法的伪代码如下：

# 实验

数据集和模型

• CIFAR-10：WideResNet
• GTSRB：WideResNet
• ImageNet：ResNet-34

攻击基线

BadNets、Trojan attack、Blend attack、Sinusoidal signal attack (SIG)、Dynamic attack、WaNet

防御基线

Fine-pruning (FP) 、Mode Connectivity Repair (MCR) 、 Neural Attention Distillation (NAD) 、 Anti-Backdoor Learning (ABL) 、Decoupling-based backdoor defense (DBD)

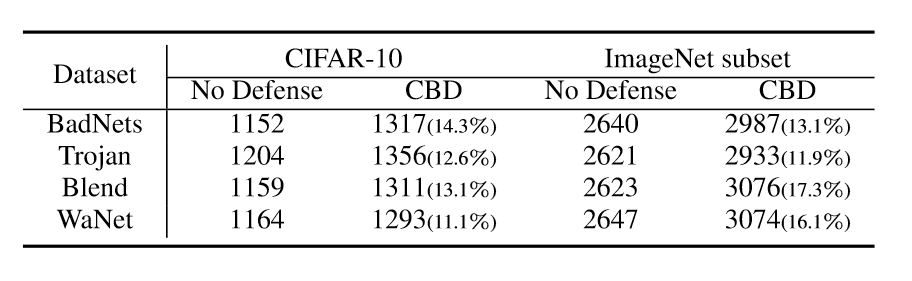
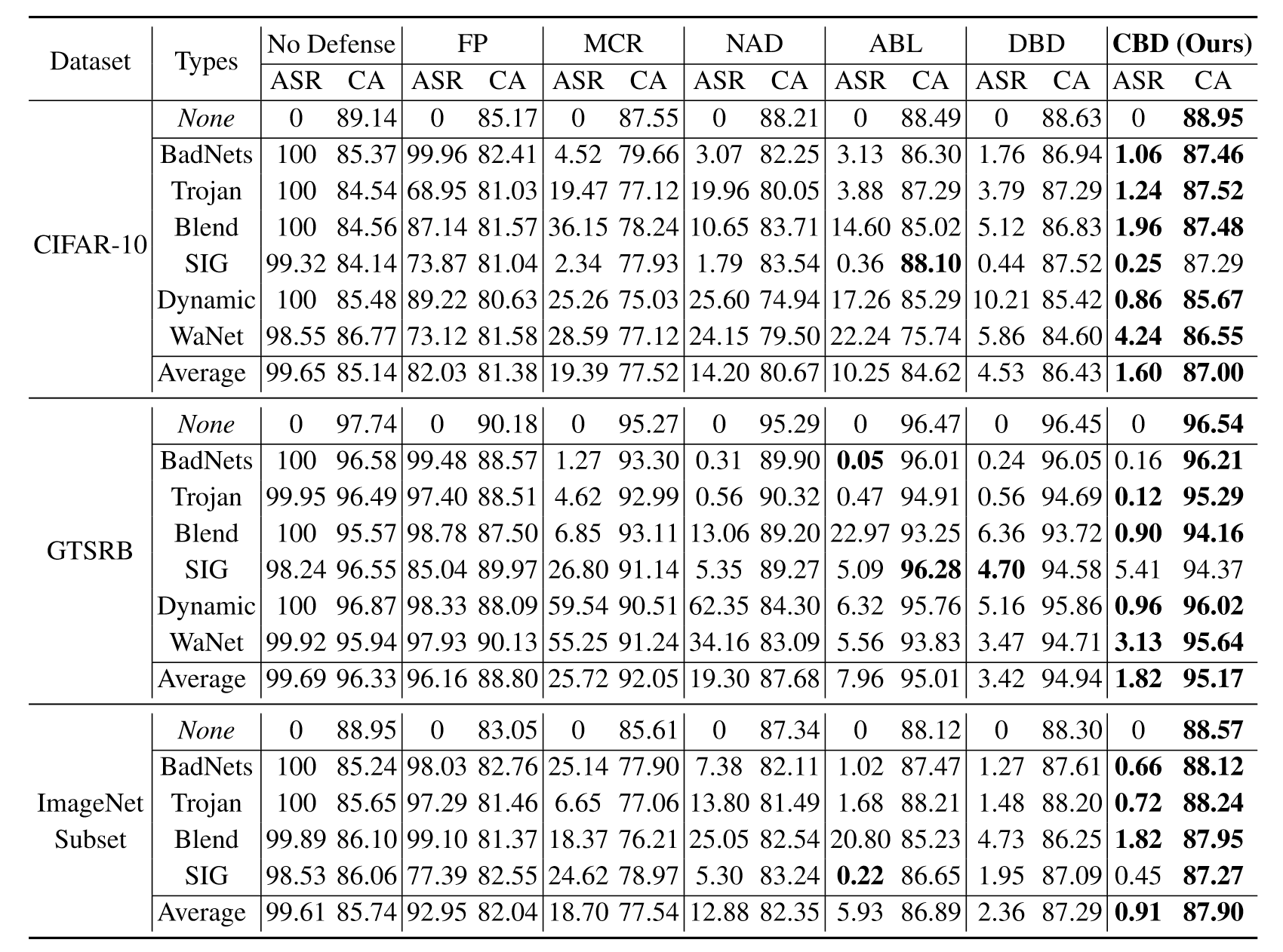
作者在10%中毒率下和其他防御方法进行了对比，证明了该方法的有效性。

同时，作者也考虑了不同中毒率下防御方法的有效性

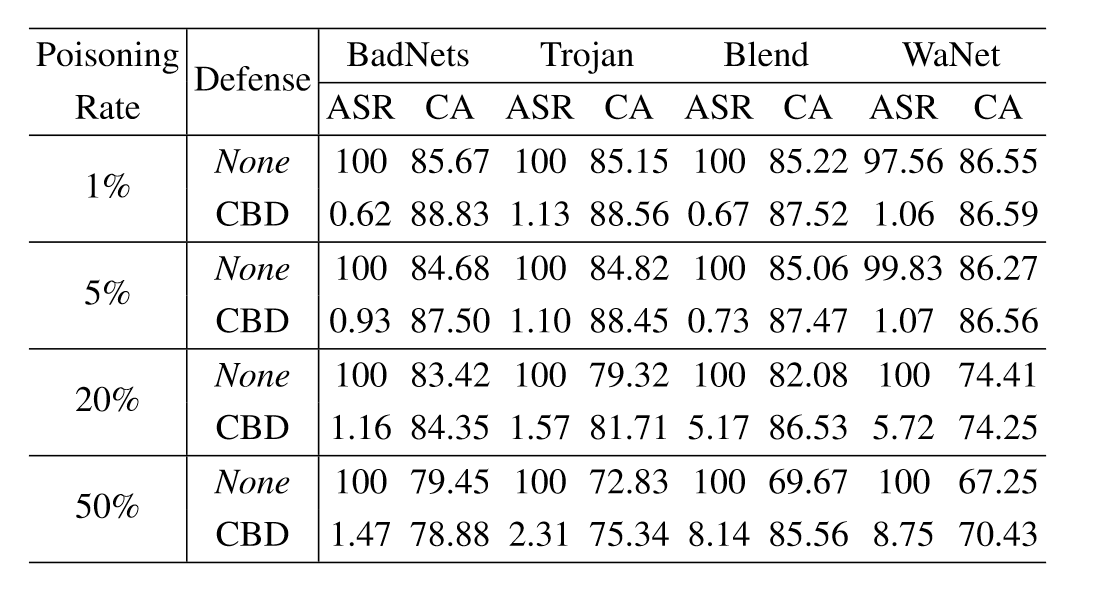
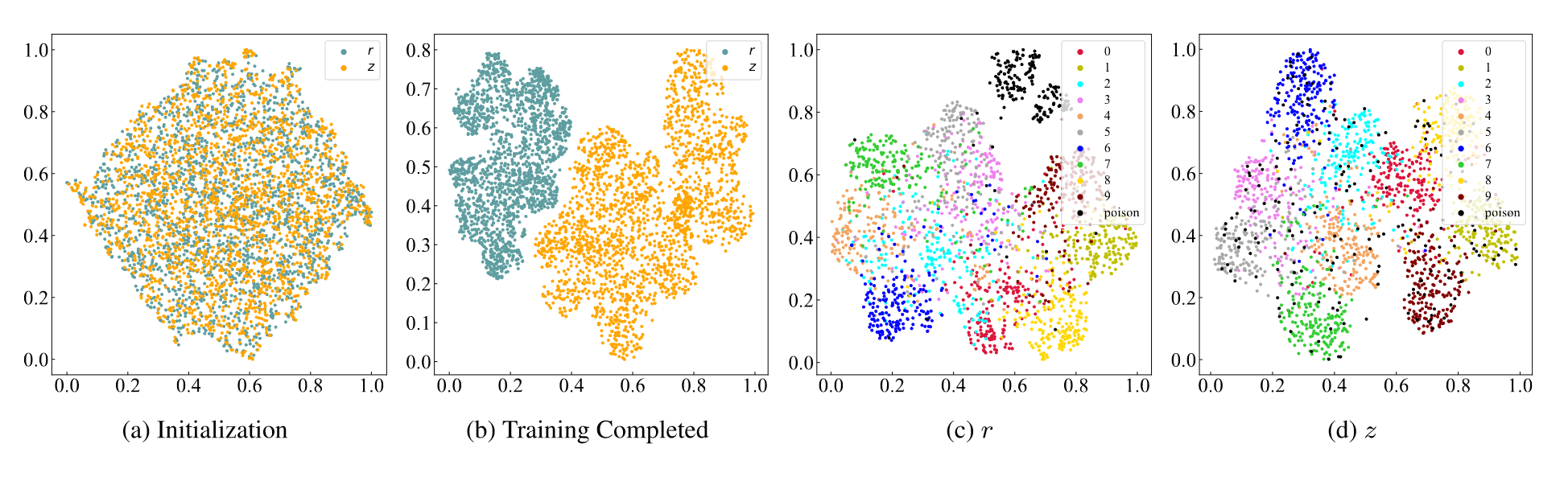
此外，作者还绘制了t-SNE图，从a和b可以看出在训练后，混杂成分$r$和因果成分$z$之间存在明显的分离。从c和d中可以看出，中毒样本的嵌入在$r$中形成簇，这表明已经学习了后门触发器和目标标签之间的虚假相关性。相比之下，中毒样本与样本密切相关，其真实标签位于去混淆嵌入$z$中，这表明CBD可以有效地防御后门攻击。

作者最后还计算了防御所需的时间，可见防御并不需要更多额外的时间