聚类算法学习笔记

Kmeans

算法步骤

从样本中选择 K 个点作为初始质心（完全随机）
计算每个样本到各个质心的距离，将样本划分到距离最近的质心所对应的簇中
计算每个簇内所有样本的均值，并使用该均值更新簇的质心
重复步骤 2 与 3 ，直到达到以下条件之一：
- 质心的位置变化小于指定的阈值（默认为 0.0001）
- 达到最大迭代次数

欧氏距离

衡量的是多维空间中两个点之间的绝对距离

在二维和三维空间中的欧氏距离就是两点之间的实际距离

计算方法：对应坐标值相减的平方和再开方

dist(X,Y)=\sqrt{\sum_{i=1}^{n}(x_i-y_i)^2}

对于二维来说，就是

dist(X,Y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}

注意理解输入？输出？类别中心？迭代过程中做什么？

编程实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
%% 生成测试数据
clear
p=100;                  % 每簇的样本数
sigma = [0.1 0;0 0.1];  % 协方差矩阵
R = chol(sigma);
% 生成测试数据集
data=[...
    [0 0] + randn(p,2)*R,1*ones(p,1);...
    [0 2] + randn(p,2)*R,2*ones(p,1);...
    [2 0] + randn(p,2)*R,3*ones(p,1);...
    [2 2] + randn(p,2)*R,4*ones(p,1);...
    ];
%% 绘制样本散点图
figure(1)
scatter(data(:,1),data(:,2),'r.')
title("无样式样本散点图")
X=data(:,1:end-1);
g=data(:,end);
n=size(X,1);
%% K-means实现
k=4;    % 指定分成的簇数

%从n个数据样本中不重复地随机选择k个样本作为质
centerIndex = randperm(n, k);
C = X(centerIndex, :);

result = struct('y',[],'C',[],'objectives',[]);
iter = 0;
maxIter = 10;   % 指定最大迭代的次数
while (iter < maxIter)
    iter = iter + 1;

    % 求出每个样本到中心点的距离，按照距离自身最近的中心点进行聚类
    D = pdist2(X, C);
    [d, ypred] = min(D, [], 2);

    % 保存结果
    result(iter).y = ypred;
    result(iter).C = C;
    result(iter).objectives = sum(d.*d);

    % 当距离没变时结束迭代
    if(iter > 1 && result(iter).objectives == result(iter-1).objectives)
        break;
    end

    % 依据上次聚类结果，求出新的中心点
    for cid = 1: size(C,1)
        C(cid, :) = mean (X(ypred == cid, :));
    end
end
%% 绘制结果散点图
figure(2);
for t = 1: numel(result)
    figure(2);
    clf
    % 绘制聚类结果
    gscatter(X(:,1), X(:,2), result(t).y,'rgbm');
    hold on;
    Ct = result(t).C;
    % 绘制聚类中心
    h=gscatter(Ct(:,1), Ct(:,2), (1: size(Ct,1)), 'kkkk', 'x+od', 10);
    title("第"+t+"次迭代后散点图")
    set(h,'LineWidth', 2.0);
    waitforbuttonpress;
    %pause(1);
end
%% 计算误差
% 输出混淆矩阵
confusionmat(g,ypred)

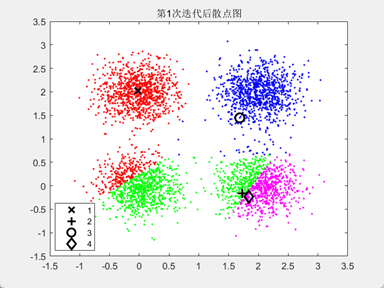
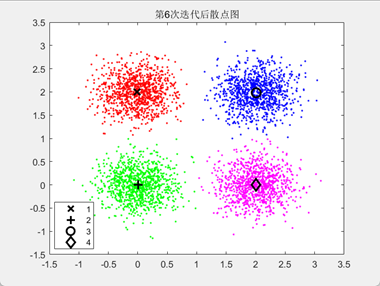
缺点

容易受初始质心的影响；算法聚类时，容易产生空簇；算法可能收敛到局部最小值。

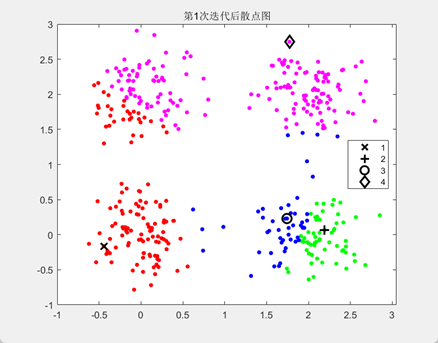
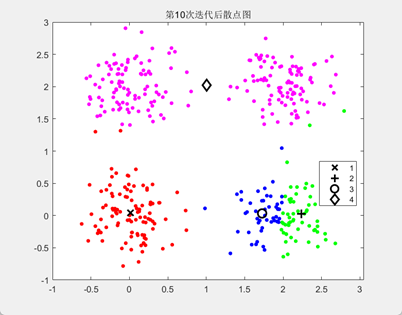
解决办法：重新执行K-means算法，重新分配质心

谱聚类(Spectral Clustering)

算法思想

把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

度矩阵D

对于一个图 $G$ ，我们一般用点的集合 $V$ 和边的集合 $E$ 来描述。即为 $G(V,E)$ 。其中 $V$ 即为我们数据集里面所有的点 $(v_1, v_2,…v_n)$ 。对于 $V$ 中的任意两个点，可以有边连接，也可以没有边连接。我们定义权重 $w_{ij}$ 为点 $v_i$ 和点 $v_j$ 之间的权重。由于我们是无向图，所以 $w_{ij} = w_{ji}$ 。

对于有边连接的两个点 $v_i$ 和 $v_j$ ， $w_{ij} > 0$ ,对于没有边连接的两个点 $v_i$ 和 $v_j$ ， $w_{ij} = 0$ 。对于图中的任意一个点 $v_i$ ，它的度 $d_i$ 定义为和它相连的所有边的权重之和，即

d_i = \sum\limits_{j=1}^{n}w_{ij}

利用每个点度的定义，我们可以得到一个nxn的度矩阵 $D$ ,它是一个对角矩阵，只有主对角线有值，对应第i行的第i个点的度数，定义如下：

\mathbf{D} = \left( \begin{array}{ccc} d_1 & \ldots & \ldots \\\\ \ldots & d_2 & \ldots \\\\ \vdots & \vdots & \ddots \\\\ \ldots & \ldots & d_n \end{array} \right)

利用所有点之间的权重值，我们可以得到图的邻接矩阵 $W$ ，它也是一个nxn的矩阵，第i行的第j个值对应我们的权重 $w_{ij}$ 。

除此之外，对于点集 $V$ 的的一个子集 $A \subset V$ ，我们定义：

|A|: = 子集A中点的个数

vol(A): = \sum\limits_{i \in A}d_i

相似矩阵

构建邻接矩阵 $W$ 的方法有三类：

$\epsilon$ -邻近法
它设置了一个距离阈值 $\epsilon$ ，然后用欧式距离 $s_{ij}$ 度量任意两点 $x_i$ 和 $x_j$ 的距离。然后根据 $s_{ij}$ 和 $\epsilon$ 的大小关系，来定义邻接矩阵 $W$ 。距离小于 $\epsilon$ 为 $\epsilon$ ，距离大于 $\epsilon$ 为0
K邻近法
利用KNN算法遍历所有的样本点，取每个样本最近的k个点作为近邻，只有和样本距离最近的k个点之间的 $w_{ij} > 0$ 。但是这种方法会造成重构之后的邻接矩阵W非对称。
全连接法（最常用）
相比前两种方法，第三种方法所有的点之间的权重值都大于0，因此称之为全连接法。可以选择不同的核函数来定义边权重，常用的有多项式核函数，高斯核函数和Sigmoid核函数，最常用的是高斯核函数RBF。

w_{ij}=s_{ij}=exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})

💡 exp(x)表示 $e^x$

拉普拉斯矩阵

拉普拉斯矩阵 $L= D-W$

$D$ 即为度矩阵，它是一个对角矩阵。 $W$ 为邻接矩阵。

无向图切图

对于无向图 $G$ 的切图，我们的目标是将图 $G(V,E)$ 切成相互没有连接的k个子图，每个子图点的集合为： $A_1,A_2,..A_k$ ，它们满足 $A_i \cap A_j = \emptyset$ ,且 $A_1 \cup A_2 \cup … \cup A_k = V$ .

对于任意两个子图点的集合 $A, B \subset V$ , $A \cap B = \emptyset$ , 我们定义A和B之间的切图权重为：

W(A, B) = \sum\limits_{i \in A, j \in B}w_{ij}

最小化切图
$\min cut(A,B)=\sum\limits_{i \in A, j \in B}w_{ij}$
RatioCut切图
$RatioCut(A,B)=cut(A,B)(\frac{1}{|A|}+\frac{1}{|B|})$
Ncut切图
$Ncut(A,B)=cut(A,B)(\frac{1}{vol(A)}+\frac{1}{vol(B)})$

算法流程

最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式，最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。

输入：样本集D= $(x_1,x_2,…,x_n)$ ，相似矩阵的生成方式, 降维后的维度 $k_1$ , 聚类方法，聚类后的维度 $k_2$

输出：簇划分 $C(c_1,c_2,…c_{k_2})$ .

根据输入的相似矩阵的生成方式构建样本的相似矩阵S
根据相似矩阵S构建邻接矩阵W，构建度矩阵D
计算出拉普拉斯矩阵L
构建标准化后的拉普拉斯矩阵 $D^{-1/2}LD^{-1/2}$
计算 $D^{-1/2}LD^{-1/2}$ 最小的 $k_1$ 个特征值所各自对应的特征向量 $f$
将各自对应的特征向量 $f$ 组成的矩阵按行标准化，最终组成 $n \times k_1$ 维的特征矩阵F
对F中的每一行作为一个 $k_1$ 维的样本，共n个样本，用输入的聚类方法进行聚类，聚类维数为 $k_2$
得到簇划分 $C(c_1,c_2,…c_{k_2})$

编程实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
rng('default')
%% 生成测试数据
p= 200;
theta = linspace(0,2*pi,p)';
data =[...
    2*[cos(theta) sin(theta)]+ rand(p,1),1*ones(p,1);
    4*[cos(theta) sin(theta)]+ rand(p,1),2*ones(p,1);
    ];
X = data(:,1:end-1);
y = data(:,end);
gscatter(X(:,1),X(:,2),y,'rg');
%% 距离矩阵
Q = pdist2(X, X);
imagesc(Q);
colorbar;
%% 构造图的相似度矩阵A
sigma = 0.1;
A = exp(-Q.*Q / (2*sigma*sigma));
imagesc(A);
colorbar;
%% 构造图的拉普拉斯矩阵L
D = diag(sum(A,2));
L = D - A;
imagesc(L);
colorbar;
%% 对拉普拉斯矩阵进行特征值分解
[V,S] = eig(L);
s = diag(S);
plot(s);
%% 取最小的k个特征值对应的特征向量
k = 2;
Vr = V(:,1:k);
Vr([1:2, end-1:end],:)
%% 对映射后的特征矩阵Vr进行kmeans聚类
idx = kmeans(Vr,k);
gscatter(X(:,1),X(:,2),idx,'rg');
title(['谱聚类 \sigma = ',num2str(sigma)])

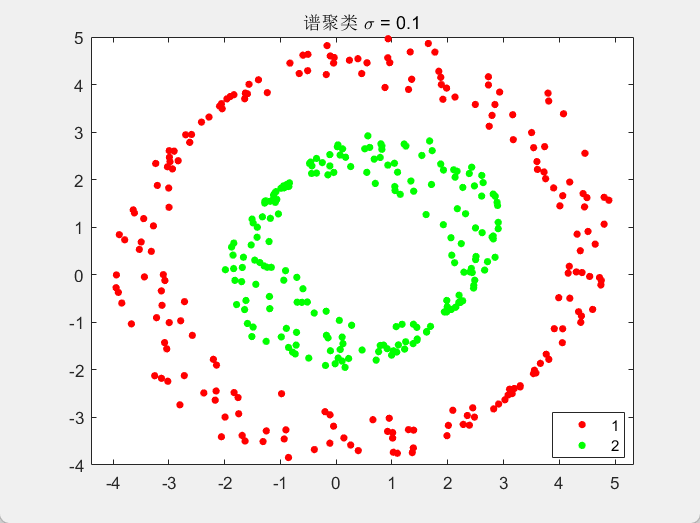
简化考试专用代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
% 数据为X,y
%% 距离矩阵
Q = pdist2(X, X);
%% 构造图的相似度矩阵A
sigma = 0.1;
A = exp(-Q.*Q / (2*sigma*sigma));
%% 构造图的拉普拉斯矩阵L
D = diag(sum(A,2));
L = D - A;
%% 对拉普拉斯矩阵进行特征值分解
[V,S] = eig(L);
%% 取最小的k个特征值对应的特征向量
k = 2;
Vr = V(:,1:k);
%% 对映射后的特征矩阵Vr进行kmeans聚类
idx = kmeans(Vr,k);

gscatter(X(:,1),X(:,2),idx,'rg');
title(['谱聚类 \sigma = ',num2str(sigma)])