回归分析学习笔记

# 线性回归

线性回归遇到的问题一般是这样的。我们有m个样本，每个样本对应于n维特征和一个结果输出，如下：

$$ (x_1^{(0)}, x_2^{(0)}, …x_n^{(0)}, y_0), (x_1^{(1)}, x_2^{(1)}, …x_n^{(1)},y_1), … (x_1^{(m)}, x_2^{(m)}, …x_n^{(m)}, y_m) $$

我们的问题是，对于一个新的$(x_1^{(x)}, x_2^{(x)}, …x_n^{(x)})$, 他所对应的$y_x$是多少呢？如果这个问题里面的y是连续的，则是一个回归问题，否则是一个分类问题。

对于n维特征的样本数据，如果我们决定使用线性回归，那么对应的模型是这样的：

$h_\theta(x_1, x_2, …x_n) = \theta_0 + \theta_{1}x_1 + … + \theta_{n}x_{n}$, 其中$\theta_i$ (i = 0,1,2… n)为模型参数，$x_i$ (i = 0,1,2… n)为每个样本的n个特征值。这个表示可以简化，我们增加一个特征$x_0 = 1$，这样$h_\theta(x_0, x_1, …x_n) = \sum\limits_{i=0}^{n}\theta_{i}x_{i}$。

💡 均方误差(MSE)

$$ MSE=\frac{1}{n}\sum_{i=1}^{m}w_i(y_i-\widehat{y_i})^2 $$

其中$y_i$是真实数据，$\widehat{y_i}$是拟合的数据，$w_i>0$

得到了模型，我们需要求出需要的损失函数，一般线性回归我们用 均方误差(MSE) 作为损失函数。损失函数的代数法表示如下：

$$ J(\theta_0, \theta_1…, \theta_n) = \sum\limits_{i=1}^{m}(h_\theta(x_0^{(i)}, x_1^{(i)}, …x_n^{(i)}) - y_i)^2 $$

由于矩阵形式不好理解，这里就不列出了。

如何求损失函数最小化时候的$\mathbf{\theta}$参数，这时就需要使用梯度下降法了。

# 梯度下降法

# 梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。那么这个梯度向量求出来有什么意义呢？他的意义从几何意义上讲，就是函数变化增加最快的地方。

# 梯度下降的直观解释

首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

梯度下降

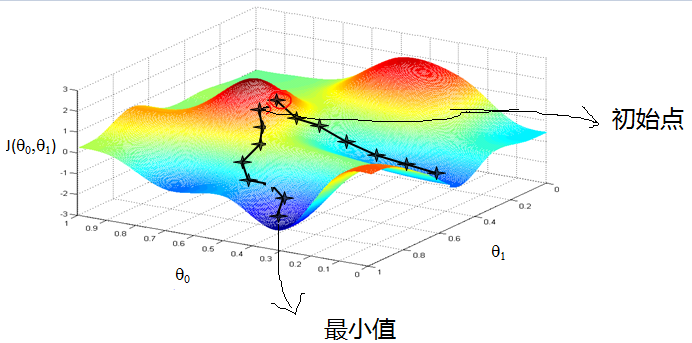
# 梯度下降法的代数方式描述

在上面的内容中，我们知道了线性回归的函数为：

$$ h_\theta(x_0, x_1, …x_n) = \sum\limits_{i=0}^{n}\theta_{i}x_{i} $$

损失函数为：

$$ J(\theta_0, \theta_1…, \theta_n) = \sum\limits_{i=1}^{m}(h_\theta(x_0^{(i)}, x_1^{(i)}, …x_n^{(i)}) - y_i)^2 $$

算法相关参数初始化：主要是初始化$\theta_0, \theta_1…, \theta_n$ ,算法终止距离$\varepsilon$ 以及步长$\alpha$ 。在没有任何先验知识的时候，我喜欢将所有的$\theta$ 初始化为0，将步长初始化为1，在调优的时候再优化。

算法过程：

确定当前位置的损失函数的梯度，对于$\theta_i$ ,其梯度表达式如下：

$$ \frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1…, \theta_n)= \frac{1}{m}\sum\limits_{j=0}^{m}(h_\theta(x_0^{(j)}, x_1^{(j)}, …x_n^{(j)}) - y_j)x_i^{(j)} $$
用步长乘以损失函数的梯度，得到当前位置下降的距离，即 $\alpha\frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1…, \theta_n)$ 对应于前面登山例子中的某一步。
确定是否所有的 $\theta_i$ ,梯度下降的距离都小于 $\varepsilon$ ，如果小于 $\varepsilon$ 则算法终止，当前所有的 $\theta_i$ (i=0,1,…n)即为最终结果。否则进入步骤4.
更新所有的$\theta$ ，对于 $\theta_i$ ，其更新表达式如下。更新完毕后继续转入步骤1.

$$ \theta_i = \theta_i - \alpha\frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1…, \theta_n) = \theta_i - \alpha (h_\theta(x_0^{(j)}, x_1^{(j)}, …x_n^{(j)}) - y_j)x_i^{(j)} $$

从这个例子可以看出当前点的梯度方向是由所有的样本决定的，加 $\frac{1}{m}$ 是为了好理解。由于步长也为常数，他们的乘机也为常数，所以这里 $\alpha\frac{1}{m}$ 可以用一个常数表示。

在下面第4节会详细讲到的梯度下降法的变种，他们主要的区别就是对样本的采用方法不同。这里我们采用的是用所有样本。

# 随机梯度下降法(SGD)

随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。对应的更新公式是

$$ \theta_i = \theta_i - \alpha (h_\theta(x_0^{(j)}, x_1^{(j)}, …x_n^{(j)}) - y_j)x_i^{(j)} $$

随机梯度下降法，和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

# 编程实现

网上找的代码，没验证，看个思路就行

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


function [ theta,J_history ] = StochasticGD( X, y, theta, alpha, num_iter )
m = length(y);
J_history = zeros(20, 1);
temp = 0;
n = 0;
for iter = 1:num_iter
     temp = temp + 1;
     index = randi(m);
     theta = theta -alpha *  (X(index, :) * theta - y(index)) * X(index, :)';
     if temp>=100
         temp = 0;
         n = n + 1;
         J_history(n) = ComputeCost(X, y, theta);
     end
end
end

# 小批量梯度下降法(Mini-Batch SGD)

也就是对于m个样本，我们采用x个样子来迭代，1<x<m。一般可以取x=10，当然根据样本的数据，可以调整这个x的值。

# 岭回归

~~助教妹说就是不考~~ 反转了，居然要考

在原先的线性回归的代价函数上加入了一个L2正则项，就是岭回归

$$ J(\theta_0, \theta_1…, \theta_n) = \sum\limits_{i=1}^{m}(h_\theta(x_0^{(i)}, x_1^{(i)}, …x_n^{(i)}) - y_i)^2+\lambda \sum_{i=1}^m\theta_i^2 $$

# 非线性形式

助教妹说就是不考