Featured image of post 初探区间求和问题
算法

初探区间求和问题

记录我对前缀和、差分、树状数组的认识

最近看了很多篇关于如何刷题的文章，其中都不约而同的提到了"总结"这个关键词。仔细想想自己确实是从来没有做过一篇总结，刷过的题目就过去了，导致同样的题目再做一次又不会了。

我的第一篇总结就以最近刷到的「区间求和」问题展开吧。首先，先上一般问题的模板（其中加粗的为最佳方案）：

  • 数组不变，区间查询：前缀和、树状数组、线段树；
  • 数组单点修改，区间查询：树状数组、线段树；
  • 数组区间修改，单点查询：差分、线段树；
  • 数组区间修改，区间查询：线段树。

# 前缀和

前缀和的作用就是为了帮助我们快速求某一段的和，是「差分」的逆运算。

前缀和数组的每一位记录的是当前位置距离起点位置，这连续一段的和区间和。

# 一维前缀和

假设有一个一维数组$x$和该数组的一维前缀和数组$y$，则$x$和$y$满足以下关系：

$$y_0=x_0、y_1=x_0+x_1、y_2=x_0+x_1+x_2、……、y_n=x_0+x_1+…+x_n$$

所以我们可以通过 $y_n=y_{n-1}+x_n$ 这个公式计算出前缀和，代码实现如下：

1
2
3
4

for (int i = 0; i < n; i++) {
    if (i == 0) y[i] = x[i];
    else y[i] = y[i - 1] + x[i];
}

但是在实际使用中，常常会遇到左边界溢出的情况，为了避免这种情况，我们可以将前缀和数组整体向后移动一位，下面给出前缀给计算代码：

1
2
3
4

int n = x.size();
vector<int> y(n + 1);
for (int i = 1; i <= n; i++)
    y[i] = y[i - 1] + x[i - 1];

这样当我们想求区间$[a,b]$之和时只需要计算$y[b+1]-y[a]$即可。

# 二维前缀和

有一个二维数组$a$和该数组的二维前缀和数组$b$（其同样是个二维数组)

右侧标注橙色的二维前缀和元素，其值是左侧的原二维数组中标注橙色的所有元素的和。

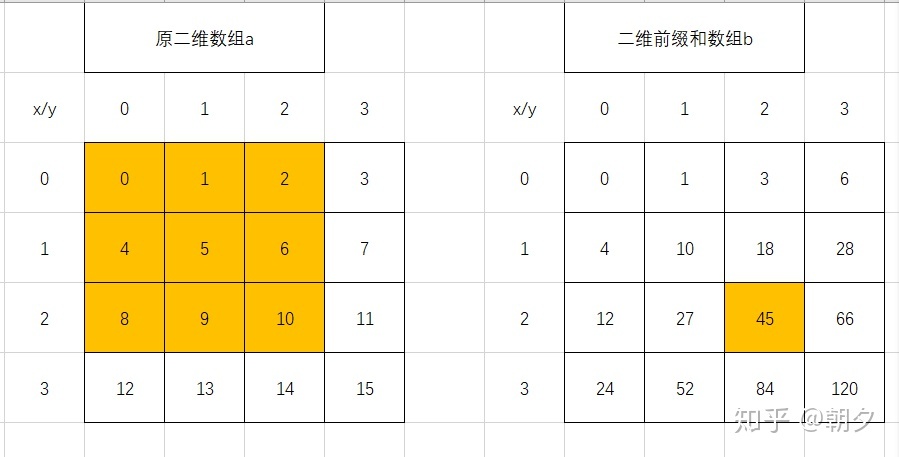
二维前缀和

二维前缀和实际上就是一个矩阵内值的和，而矩阵又可以由两个行数或列数少一的子矩阵组合后，删去重合部分再加上右下角的值来构成，也就是以下式子：

$$b_{x,y}=b_{x-1,y}+b_{x,y-1}-b_{x-1,y-1}+a_{x,y}$$

详细的代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

for (int y = 0; y < n; y++)      // n行
    for (int x = 0; x < m; x++)  // m列
    {
        if (x == 0 && y == 0)
            b[y][x] = a[y][x];  //左上角的值
        else if (x == 0)
            b[y][x] = b[y - 1][x] + a[y][x];  //第一列
        else if (y == 0)
            b[y][x] = b[y][x - 1] + a[y][x];  //第一行
        else
            b[y][x] = b[y - 1][x] + b[y][x - 1] - b[y - 1][x - 1] + a[y][x];
    }

通过二维前缀和，我们可以很方便的计算出给定矩阵的和，即上面求前缀和的逆运算。假设所求矩阵的左上角点为$(x1,y1)$，右下角点为$(x2,y2)$，则有公式：

$sum=B[y2][x2]+B[y1-1][x1-1]-B[y1-1][x2]-B[y2][x1-1]$

这里结合图形会更好理解一点。

# 例题

力扣303. 区域和检索 - 数组不可变

就是一维前缀和的模板题，直接上模板即可做出。

# 差分

差分是一种处理数据的巧妙而简单的方法，它应用于区间的修改和询问问题。如果我们要经常对数组A某个区间内的所有元素做相同的加减操作，如果一个一个修改效率很差，但是使用差分数组后，这个操作的时间复杂度就能降到$\Omicron(1)$,当所有的修改操作结束后，再利用差分数组，计算出新的A。

# 一维差分

我们定义原数组为$a[]$、差分数组为$D[]$，则有计算公式：$D[k]=a[k]-a[k-1]$,即原数组$a[]$的相邻元素的差。从定义我们可以推出$a[k]=D[0]+D[1]+…+D[k]$。也就是说$a[]$是$D[]$的前缀和，所以「差分」和「前缀和」就是一组逆运算。

当我们想要对区间$[L,R]$每个元素加上$d$，则只要进行下面的两步操作：

1
2

D[L] += d;
D[R+1] -= d;

当所有修改都完成时，我们可以通过复杂度为$\Omicron(n)$的操作计算出新的$a[]$

当然，差分也不是万能的，它只能解决 区间修改+单点查询 这类问题。当遇到需要多次查询的问题，比如有$m$次修改，$k$次查询，此时修改的复杂度为$\Omicron(m)$,查询的复杂度为$\Omicron(kn)$，总复杂度为$\Omicron(m+kn)$，和暴力法$\Omicron(mn+k)$的复杂度一致了。

# 二维差分

从一维差分可以很容易的推广到二维差分，我们可以通过下面的公式计算$D[][]$：

$$D[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$$

我们想修改坐标点$(x1,y1)$~$(x2,y2)$定义的区间，则需要修改矩阵的四个点：

1
2
3
4

D[y1][x1]     += d;     //二维区间的起点
D[y1][x2+1]   -= d;     //把y看成常数，x从x1到x2+1
D[y2+1][x1]   -= d;     //把x看成常数，y从y1到y2+1
D[y2+1][x2+1] += d;     //由于前两式把d减了2次，多减了1次，这里加1次回来

前缀和$a[][]$的计算可以用下面的公式：

$$a[i][j]=D[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1]$$

在计算$a[][]$时，我们可以不新开一个数组，而是以用过的$D[][]$作为$a[][]$，以此来节约空间。使用的话只需要将上面式子中的$a$全部换为$D$

# 树状数组

树状数组的优点在于查询和修改的时间复杂度都为$\Omicron(logn)$，且比线段树好写。

# 单点修改、区间查询

树状数组的原理由于时间有限，这里就不展开说了（之后有空再补上😇），先上模板：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

int c[MAXN];	//树状数组(下标从1开始)
int n;			//数组的长度

inline int lowbit(int i) {
    return i & (-i);
}

//在位置i加上k
void update(int i, int k) {
    while (i <= n) {
        c[i] += k;
        i += lowbit(i);
    }
}

//求A[1]~A[i]的和
int getsum(int i) {
    int res = 0;
    while (i > 0) {
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

这里一定要注意，树状数组和原数组下标都是从1开始的。

由此就解决了单点修改、区间查询的问题，我们想要得到区间$(a,b)$的和，只需使用getsum(b) - getsum(a - 1)。

例题：P3374【模板】树状数组 1

# 区间修改、单点查询

在上面的差分中我们分析了，如果有多次查询，仅仅使用差分的时间复杂度就和暴力差不多了。这时，我们可以采用树状数组+差分的方法。

我们将上面模板中的原始数组改为差分数组。由差分的性质可知，当我们修改一个区间时，只需要修改区间的两个端点即可，此时区间修改的问题便被转化成了单点修改的问题。同时，树状数组前n项和也就变成了原数组第n项的值。

例题：P3368【模板】树状数组 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

//前面还是树状数组的模板，这里就不放了

int main() {
    cin >> n >> m;
    int pre = 0, now;
    for (int i = 1; i <= n; i++) {
        cin >> now;
        //这里每次求差分来生成树状数组
        update(i, now - pre);
        pre = now;
    }
    while (m--) {
        int a, x, y, k;
        cin >> a >> x;
        if (a == 1) {
            cin >> y >> k;
            //更新即为对D[X]、D[y+1]进行修改
            update(x, k);
            update(y + 1, -k);
        } else if (a == 2) {
            //求D[1]~D[i]的和,即A[i]的值
            cout << getsum(x) << endl;
        }
    }
    system("pause");
    return 0;
}

# 参考资料